Теоретические сведения

Ответы

Задачи для самостоятельного решения

1. На железнодорожной станции есть 5 светофоров. Сколько может быть дано различных комбинаций их сигналов, если каждый светофор имеет два состояния?

2. Сколькими способами 10 человек могут встать в очередь друг за другом?

3. Сколько хорд можно провести через 6 точек, лежащих на одной окружности?

4. В классе 30 учеников. Ежедневно двое из них дежурят. Можно ли составить расписание дежурства так, чтобы никакие два ученика не дежурили вместе дважды в течение года?

5. У хозяйки имеется 4 чашки, 5 блюдец и 6 чайных ложек. Сколькими способами может быть накрыт стол для чаепития на трех человек?

6. В НИИ работают 67 человек. Из них 47 человек знают английский язык, 35 – немецкий язык, 23 человека знают оба языка. Сколько человек не знают ни английского, ни немецкого языка?

7. В состав сборной включены: 2 вратаря, 5 защитников, 6 полузащитников, 6 нападающих. Сколькими способами тренер может выставить команду: 1 вратарь, 3 защитника, 4 полузащитника, 3 нападающих?

8. Сколько различных «слов» можно составить, переставляя буквы слова «МИССИСИПИ»?

9. Группа шахматистов сыграла между собой 28 партий. Каждые два из них встречались между собой один раз. Сколько шахматистов участвовало в соревновании?

10. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий три торта?

11. Сколькими различными способами можно распределить поровну 12 различных учебников между четырьмя студентами?

12. Сколько имеется пятизначных чисел, все цифры у которых различны?

13. Группа туристов из 12 юношей и 7 девушек выбирает по жребию 5 человек для приготовления ужина. Сколько существует способов, при которых в эту «пятерку» попадут: а) одни девушки, б) 1 юноша и 4 девушки?

14. Сколько различных комбинаций из 6 карт содержат 3 дамы, 2 короля и 1 туза?

15. Сколько различных «слов», состоящих из трех букв, можно образовать из букв слов: а) лето, б) шалун?

1. 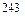комбинации, 2. 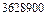способов, 3. 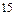хорд, 4. Можно, т. к. существует 435 способов назначения дежурных 5. 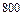способов, 6. 8 человек, 7. 6000 способов, 8. 2520 слов, 9. 8 шахматистов, 10. 84 возможности, 11. 369600 способов, 12. 27216 чисел, 13. а) 21, б) 420, 14. 96 комбинаций, 15. а) 24, б) 60.

Раздел 6. Алгебраические структуры

Бинарной алгебраической операцией на множестве М называется произвольное отображение 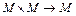, которое любой упорядоченной паре (x,y) элементов x, y ставится в соответствие однозначно определенный элемент того же множества M.

Бинарную операцию на M обозначают каким-нибудь специальным символом: 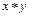, , 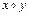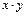или .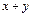

Примеры: Какие из арифметических действий - сложение, вычитание, умножение, деление – являются бинарными операциями на следующих множествах: 1) N – множество натуральных чисел; 2) Z - множество целых чисел?

Решение: 1) N – множество натуральных чисел

сложение: 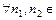N выполняется 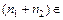N, следовательно, сложение является бинарной операцией на N

вычитание: 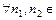N N (например, N), следовательно, вычитание не является бинарной операцией на N

умножение: 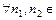N имеет место 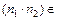N, следовательно, умножение – бинарная операция

деление: (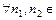 N) N 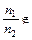(например, N), следовательно, деление – не бинарная операция.

2) Z – множество целых чисел:

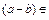Z имеет место Z, Z, 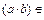Z, сложение, вычитание и умножение являются бинарными операциями на множестве целых чисел. Но 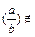Z, следовательно, деление не является бинарной операцией.

На множестве M может быть задано вообще говоря, много разных операцией. Желая выделить одну из них, используют скобки 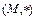и говорят, что операция 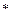определяет на M алгебраическую структуру, или что 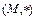- алгебраическая структура ( алгебраическая система ).

Так, например, на множестве Z целых чисел помимо естественных операций +, · (сложение и умножение) легко указать получающиеся при помощи +, -, · «операции»: 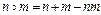, 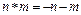и т.д. Таким образом, мы приходим к различным алгебраическим структурам (Z, +), (Z,·), (Z, 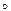), (Z, ).

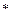Бинарная операция 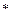на множестве A называется коммутативной, если для любых двух элементов 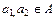выполняется .

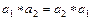Операция 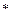определенная на множестве A называется ассоциативной, если для любых трех элементов из множества A выполнено .

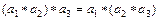Пусть на множестве A задана операция 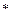. Если существует такой элемент 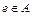, что для любого элемента 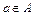выполняется 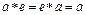, то элемент называют ( нейтральным ), единичным.

Если нейтральный элемент существует, то он единственный.

Элемент b из множества A называется обратным к элементу a из того же самого множества, есл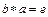и и .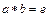

Обратные элементы используются для построения обратных операций.

Пусть на множестве задана операция 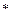. Эта операция называется обратимой, если для любых элементов a,b из множества A каждое из уравнений 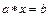, 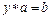имеет единственное решение в множестве A.

Примеры:

I алгебраическая система (R, +, 0), здесь 0 – нейтральный элемент

II алгебраическая система (R₊, ·,1), 1 – нейтральный элемент.

Множество G элементов произвольной природы с заданной на нем бинарной операцией 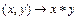: 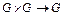(ее чаще всего называют умножением), называется группой, если выполнены следующие аксиомы:

1) ассоциативность: для любых ;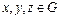

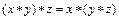2) наличие нейтрального элемента: в G существует элемент e, такой что для всех x из G справедливо ;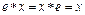

3) обратный элемент: для каждого x из G найдется элемент x ^-1 из G, называемый обратным, такой, что .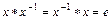

Часто используют одну из двух терминологий:

1) 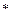– умножение. Тогда группу называют мультипликативной группой. В этом случае e – единица, g^-1- обратный элемент

2) 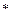- сложение. Тогда группу называют аддитивной группой. Здесь e =0, (-g) – противоположный элемент.

Если для любых 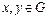выполняется , то группа 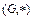называется коммутативной или абелевой.

Группу, состоящую из конечного числа элементов, называют конечной, а число элементов в ней – порядком группы и обозначают 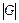, и бесконечной, если множество элементов бесконечно.

Подмножество 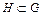называется подгруппой в группе G, если это подмножество само является группой относительно той же бинарной операции:

1) ;

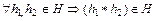2) ;

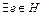3) /

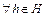
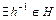Подгруппа 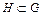– собственная, есл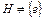и и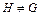

Примеры: Выясните, какие из нижеприведенных множеств являются группами относительно указанных операций:

1. (R, +, 0)

Проверяем является ли эта система группой: 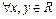выполняется 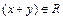. Следовательно, сложение является бинарной операцией на. Проверяем аксиомы:

1) ассоциативность: 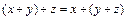выполняется;

2) 0- нейтральный элемент: 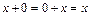- выполняется

3) Обратный элемент: 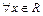существует 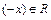так что 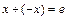– выполняется.

Следовательно, (R, +, 0) является группой.

2. М – множество невырожденных матриц второго порядка относительно операции умножения: 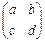, где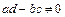

Для любых матриц А,В 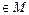имеет место 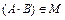. Проверяем аксиомы:

1) ассоциативность: произведение матриц ассоциативно, т.е. для любых матриц 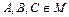выполняется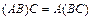

2) в качестве нейтрального элемента возьмем 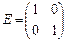- единичную матрицу. В самом деле 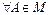имеет место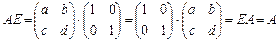

3) наличие обратного элемента: для любой невырожденной матрицы (det A = ad-bc 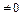) существует обратная матрица: , где А _11, А _12, А _21, А ₂₂ – алгебраические дополнения. Следовательно, множество невырожденных матриц второго порядка относительно операции умножения является группой. Однако операция умножения матриц не является коммутативной (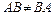). Поэтому данная группа не является коммутативной.

3. Множество целых чисел Z относительно вычитания./

Проверим, что операция «вычитание» является бинарной: 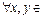Z имеет место 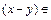Z. Проверяем выполнимость аксиом:

1) Ассоциативность: 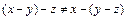. Видим, что первая аксиома ассоциативности не выполняется.

Следовательно, множество целых чисел с заданной операцией «вычитание» не является группой.

4. Множество четных чисел относительно операции умножения.

Произведение четных чисел является четным числом: (2 k₁k ₂=2·2 k₁k₂). Поэтому проверим выполнимость аксиом:

1) Ассоциативность: 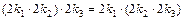- выполняется;

2) Наличие нейтрального элемента: 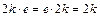. При операции «умножение» этому условию удовлетворяет нейтральный элемент 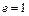. Но 1 не принадлежит множеству четных чисел. Следовательно, аксиома о наличии нейтрального элемента не выполняется.

Поэтому, множество четных чисел с операцией «умножение» не является группой.

Дата добавления: 2014-12-27