Постановка задачи. Тема 6.4. Численное интегрирование

Тема 6.4. Численное интегрирование

Применить кубическую сплайн-интерполяцию, при которой экспериментальные точки соединяются отрезками кубических полиномов.

Для этого одновременно используются две функции: interp(s,x,y,t ) и cspline(x,y), где x – вектор значений аргументов, y – вектор значений функции, s – вектор вторых производных, создаваемый функцией cspline, t – значение аргумента, при котором вычисляется функция.

 

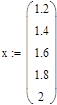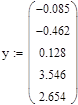
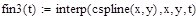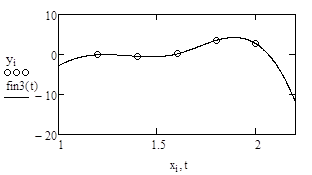
6.4.1. Постановка задачи

6.4.2. Метод прямоугольников

6.4.3. Формула трапеций

6.4.4. Формула Симпсона

6.4.5. Оценка погрешности численного интегрирования

6.4.6. Технология вычисления интегралов в среде математических пакетов

Из курса математического анализа известно, что, если функция f(x) непрерывна на отрезке [a;b] и дифференцируема, то определенный интеграл от этой функции в пределах от a до b существует и может быть вычислен по формуле Ньютона-Лейбница:

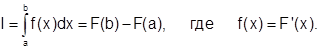
Если первообразную функцию F(x) не удается выразить аналитически через элементарные функции или если при проведении практических расчетов подынтегральная функция f(x) задается в виде таблицы, то это приводит к необходимости замены аналитического интегрирования численными методами.

Для функции f(x), заданной в прямоугольной системе координат на интервале [a;b], этот интеграл численно равен площади, ограниченной кривой f(x), осью Ox и двумя ординатами ac и bd.

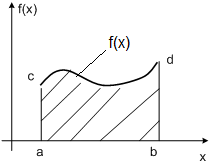
Рис. 6.4.1-1

Задача численного интегрирования заключается в нахождении значения определенного интеграла через ряд значений подынтегральной функции y_i=f(x_i), заданной в точках x_i (i=0,1,…,n). Причем, x₀ = a, x_n = b. Чаще всего интервал разбивают на подынтервалы длинойh = x_i+1 - x_i.

Применительно к однократному интегралу, формулы численного интегрирования представляют собой квадратурные формулы вида:

гдеA_i – числовые коэффициенты, называемые весами квадратурной формулы, аx_i – точки из отрезка - узлами квадратурной формулы, n > 0 – целое число.

Искомый определенный интеграл можно представить в виде суммы интегралов:

На каждом i -м отрезке функция аппроксимируется (заменяется) некоторой другой легко интегрируемой функцией g_i(x). В результате получаем следующую квадратурную формулу:

.

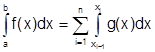Для решения поставленной задачи подынтегральную функцию f(x) необходимо заменить приближенной функцией, которая может быть проинтегрирована в аналитическим виде. В качестве такой функции обычно используют полином Р(х) с узлами интерполяции в точках х₀, х₁, х₂, …,х_n. В этих точках значения функции и интерполяционного полинома полностью совпадают f(x_i) = Р(x_i).

Для получения простых формул интегрирования используют полиномы нулевой, первой и второй степени и соответственно получают формулы численного интегрирования: прямоугольников, трапеций и Симпсона.

Очевидно, что замена функции f(x) интерполирующим полиномом приводит к образованию погрешности вычисления значения интеграла

где I₁ – точное значение интеграла, I – значение интеграла, вычисленного численным методом, а – погрешность метода.

Отметим, что увеличение числа подынтервалов n (или уменьшение длины шага интегрирования h) ведет к уменьшению погрешности.

Дата добавления: 2014-12-27