Лимитирование роста. Уравнение Моно

Ограничение удельной скорости роста называется лимитированием, а фактор, ограничивающий скорость – лимитирующим фактором.

Принцип выявления лимитирующего рост фактора состоит в следующем. Если при небольшом увеличении фактора наблюдается ответное увеличение удельной скорости роста, то данный фактор лимитирует рост; в противном случае фактор не является лимитирующим. Рост может быть лимитирован по одному или нескольким компонентам питательной среды, соответственно, говорят об однофакторном и многофакторном лимитировании.

Рост, лимитированный по концентрации одного из субстратов, описывается уравнением Моно:

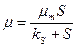, (2.8)

где 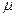- удельная скорость роста; 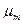– максимальная удельная скорость роста; S – концентрация субстрата; 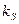– константа Моно по субстрату S, численно равная концентрации субстрата, при которой удельная скорость роста равна половине максимальной (см. рис. 2.2).

Рис. 2.2. Зависимость 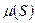по уравнению Моно

Уравнение Моно основано на теории ферментативной кинетики и принципе «узкого места» (лимитирующей стадии метаболизма); оно описывает рост простой (состоящей из одного вида) культуры на простом субстрате.

Чтобы установить соответствие экспериментальных данных уравнению Моно, а также найти значения параметров 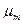и 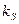, применяют его различные линеаризованные формы:

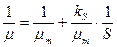; (2.9)

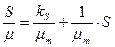; (2.10)

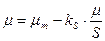. (2.11)

Чаще используют первую форму (2.9), дающую линейную зависимость 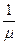от 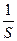(график двойных обратных величин), но более точную оценку параметров можно получить по 2-й (2.10) и 3-й (2.11) формам. Определение параметров уравнения Моно по 2-й линеаризованной форме показано на рис. 2.3.

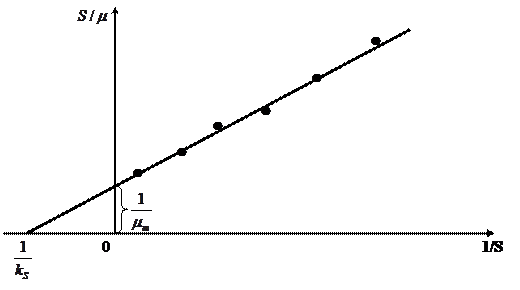
Рис. 2.3. Линеаризованная форма уравнения Моно по уравнению (2.10)

Уравнение Моно может быть распространено и на случай многофакторного лимитирования роста. Например, для нитрифицирующих бактерий, осуществляющих биоокисление аммонийного азота кислородом, справедливо уравнение:

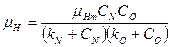, (2.12)

где 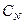, 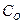- концентрации аммонийного азота и растворенного кислорода в среде; 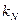, 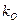- константы Моно по азоту и кислороду.

Константы Моно для бактерий имеют очень небольшие значения. Для гетеротрофов типичные значения константы Моно по органическому субстрату, 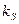=1-10 мг/л, а по кислороду (для аэробов), 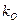=0,1-0,2 мг/л. Для нитрифицирующих бактерий, относящихся к автотрофам, 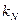=1 мг/л, 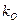==1 мг/л.

Уравнение Моно дает зависимость удельной скорости роста от концентрации субстрата на поверхности клетки. Для мелких клеток, в частности бактерий, концентрация субстрата на их поверхности практически равна концентрации субстрата в растворе, которую и измеряют на практике. Для крупных клеток и клеточных агрегатов размером порядка 0,1 мм концентрация субстрата в растворе может существенно превышать концентрацию на поверхности клетки. В этом случае зависимость скорости роста от концентрации субстрата в растворе описывается не уравнением Моно, а уравнением диффузии; соответственно, говорят о лимитировании роста по диффузии субстрата.

При лимитировании по диффузии субстрата удельная скорость роста возрастает с увеличением интенсивности перемешивания среды в силу двух причин: увеличение скорости диффузии субстрата из раствора к поверхности клеточного агрегата и уменьшение размера агрегатов, что снижает длину массопереноса внутри агрегата.

С увеличением концентрации субстрата в растворе лимитирование ростадиффузией снимается, и зависимость 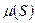приближается к таковой по уравнению Моно. Для практических целей обычно используют уравнение, формально отвечающее уравнению Моно, но включающее константу 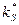, учитывающую лимитирование роста по диффузии субстрата:

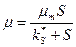, (2.13)

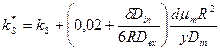, (2.14)

где 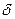- толщина жидкостной пленки вокруг клеточного агрегата, в которой перенос субстрата осуществляется за счет молекулярной диффузии (в остальной части раствора происходит быстрый перенос за счет турбулентной диффузии); 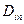, 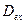- коэффициенты молекулярной диффузии субстрата внутри клеточного агрегата и вне его (в растворе); 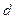- концентрация сухой биомассы в клеточном агрегате; 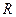- эффективный радиус клеточного агрегата; 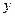- экономический коэффициент.

Размерность всех параметров в формулах (2.13) и (2.14) – в системе СИ. Нетрудно показать, что в области резкого лимитирования по диффузии удельная скорость роста целиком определяется скоростью диффузии. Действительно, при лимитировании роста только диффузией, выполняется: 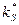>> 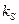, 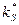>> . Соответственно, из (2.13) и (2.14) следует, что величина 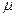не зависит от параметров 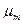и 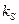, а целиком определяется параметрами процесса диффузии:

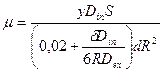. (2.15)

При увеличении интенсивности перемешивания значения параметров 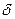и 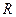уменьшаются, что влечет возрастание удельной скорости роста; величина 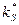снижается, приближаясь к величине 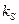, соответственно, степень лимитирования роста диффузией уменьшается (рис. 2.4).

Рис. 2.4. Зависимость 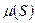по уравнению Моно (1) и при лимитировании роста по диффузии субстрата (2) по уравнению (2.13)

Дата добавления: 2014-12-27