
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диаграммы Эйлера-Венна
|
|
|
|
Операции над множествами и их свойства.
Для получения новых множеств из уже существующих используют операции над множествами. Рассмотрим основные из них.
Объединением множеств X и Y называется множество 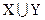 , все элементы которого являются элементами множества X или Y:
, все элементы которого являются элементами множества X или Y:
 ={ x
={ x  x
x 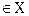 или
или 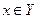 }.
}.
Пересечением множеств X и Y называется множество 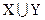 , элементы которого являются элементами обоих множеств X и Y:
, элементы которого являются элементами обоих множеств X и Y:
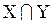 ={ x | x
={ x | x 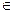 X и x
X и x 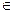 Y}.
Y}.
Очевидно, что выполняются включения
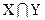
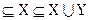 ;
; 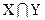

Разностью множеств X и Y называется множество  всех тех элементов X, которые не принадлежат Y:
всех тех элементов X, которые не принадлежат Y:
 ={ x
={ x 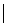 x
x 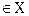 и
и  }.
}.
Дополнением множества X называется множество  всех тех элементов x, которые не принадлежат множеству X:
всех тех элементов x, которые не принадлежат множеству X:
 .
.
Симметрической разностью (или кольцевой суммой) множества X и Y называется множество
 .
.
Замечание.  .
.
Универсальное множество графически изображают в виде множества точек прямоугольника, отдельные области внутри этого прямоугольника соответствуют различным подмножествам универсального множества. Такое представление универсального множества и его подмножеств называется диаграммой Эйлера-Венна. На диаграмме Эйлера-Венна можно проиллюстрировать все основные операции над множествами (рис. 1.1-1.5).

Операции над множествами обладают определенными свойствами и удовлетворяют некоторым соотношениям. Рассмотрим следующие утверждения.
Утверждение 1.2.1. Для любых множеств X, Y, Z выполняются следующие тождества (основные свойства операций):
1. Коммутативность операций  и
и 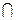 :
:
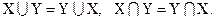
2. Ассоциативность операций  и
и 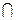 :
:

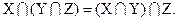
3. Законы дистрибутивности
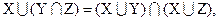

4. 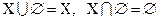 .
.
5. 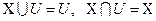 .
.
6. Законы комплиментарности: 

7. Законы идемпотентности: 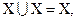

8. Законы де Моргана: 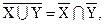
 .
.
(Август де Морган (1806–1871) – английский математик).
9. Закон двойного отрицания 
10. Законы поглощения


Докажем один из законной дистрибутивности:

Доказательство. Чтобы доказать равенство двух множеств А = В нужно доказать, что А Í В и В Í А. Докажем, что 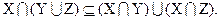 Для доказательства этого включения выберем произвольный элемент из множества
Для доказательства этого включения выберем произвольный элемент из множества 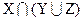 и покажем, что он принадлежит множеству
и покажем, что он принадлежит множеству 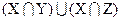 . Итак, пусть
. Итак, пусть 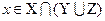 . Тогда
. Тогда  и
и 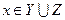 . Если
. Если 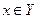 , то
, то 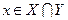 , а значит,
, а значит,  . Если
. Если 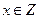 , то
, то 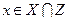 , а значит,
, а значит,  . Таким образом,
. Таким образом,
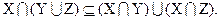
Теперь докажем, что  Пусть
Пусть  . Если
. Если 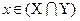 , то
, то  и
и 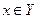 , отсюда следует, что
, отсюда следует, что  и
и 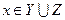 , т.е.
, т.е. 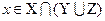 . Если
. Если  , то
, то  и
и 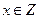 . Отсюда следует, что
. Отсюда следует, что  и
и 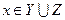 , т.е.
, т.е. 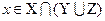 . Итак,
. Итак,  Таким образом, получили, что
Таким образом, получили, что 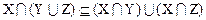 и
и 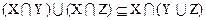 ,
,
а это значит, что эти два множества равны.
Доказательство можно оформить в более формализованном виде, используя “{” для системы высказываний, объединенных союзом “и”, “[”- для системы высказываний, объединенных союзом «или».
Докажем, один из законов де Моргана:  .
.
С одной стороны,
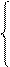



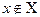





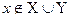
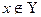
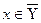
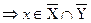
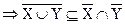 .
.
С другой стороны,

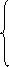
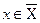

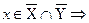


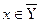


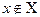
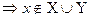
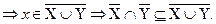
Так как 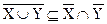 и
и  , то
, то  , что и требовалось доказать.
, что и требовалось доказать.
Утверждение 1.2.2.Следующие предложения о произвольных множествах попарно эквивалентны:
1)  ; 2)
; 2) 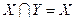 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 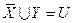 .
.
Доказательство. 1  2. Так как
2. Так как 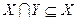 , то достаточно показать, что
, то достаточно показать, что  влечет
влечет  . Но если
. Но если  , то по условию
, то по условию  , и, следовательно,
, и, следовательно, 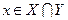 .
.
2  3. Так как
3. Так как 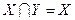 , то
, то  . По закону поглощения и закону коммутативности имеем
. По закону поглощения и закону коммутативности имеем  . Тогда
. Тогда 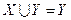 .
.
3  4. Предположим, что
4. Предположим, что 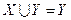 . Так как
. Так как  , то по закону де Моргана, закону ассоциативности, закону коммутативности, закону комплиментарности и закону 4 имеем
, то по закону де Моргана, закону ассоциативности, закону коммутативности, закону комплиментарности и закону 4 имеем
 .
.
4  5. Предположим, что
5. Предположим, что 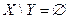 , т. е.
, т. е. 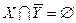 . Тогда
. Тогда 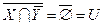 . По закону де Моргана и закону двойного отрицания получаем
. По закону де Моргана и закону двойного отрицания получаем 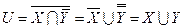 .
.
5  1. Предположим, что
1. Предположим, что  и не выполняется условие
и не выполняется условие  , т. е. найдется элемент x такой, что
, т. е. найдется элемент x такой, что  и
и  . Тогда
. Тогда  и, значит,
и, значит,  , а это противоречит равенству
, а это противоречит равенству  .
.
Отметим, что операция \ выражается через операции 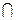 и
и  . По закону де Моргана и закону двойного отрицания справедливо соотношение
. По закону де Моргана и закону двойного отрицания справедливо соотношение 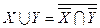 , т. е. операция
, т. е. операция  также выражается через операции
также выражается через операции 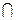 и
и  . По определению операция
. По определению операция  тоже выражается через
тоже выражается через 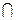 и
и  . Таким образом, любая из определенных операций над множествами выражается через операции
. Таким образом, любая из определенных операций над множествами выражается через операции 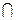 и
и  .
.
Пересечение и объединение могут быть определены для любого множества множеств  , где индексы
, где индексы 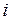 пробегают множество
пробегают множество  . Пересечение
. Пересечение 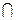 {
{  |
| 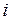 Î
Î  } и объединение
} и объединение  {
{  |
| 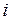 Î
Î  } задаются равенствами
} задаются равенствами
 {
{  |
| 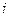 Î
Î  } = {
} = { 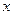 |
| 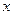 Î
Î  для всех
для всех 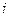 Î
Î  },
},
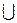 {
{  |
| 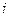 Î
Î  } = {
} = { 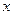 |
| 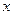 Î
Î  для некоторого
для некоторого 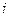 Î
Î  }.
}.
Вместо 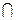 {
{  |
| 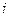 Î
Î  } и
} и  {
{  |
| 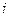 Î
Î  } часто пишут соответственно
} часто пишут соответственно 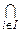
 и
и 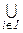
 , а иногда просто
, а иногда просто  ,
,  , если из контекста ясно, какое множество I имеется в виду. Если I = {1,2,…, n }, то
, если из контекста ясно, какое множество I имеется в виду. Если I = {1,2,…, n }, то 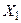
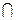

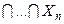 и
и 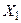

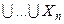 , а также
, а также 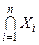 и
и 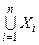 .
.
Совокупность множеств  называется покрытием множества X, если
называется покрытием множества X, если 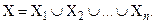 Если при этом
Если при этом  >0 и
>0 и  для всех i
для всех i  , то
, то  называется разбиением множества X.
называется разбиением множества X.
Пример. Пусть X ={ a, b, c, d, e, f }. Тогда {{ a, b, d }, { c, f }, { e }} – разбиение множества X, а {{ a, b, d }, { в, c, f }, { в, e }} – покрытие множества X.
Одним из важных понятий теории множеств является понятие декартова произведения множеств. Декартовым (прямым) произведением множеств X и Y называется множество упорядоченных пар вида
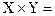 {(x, y)
{(x, y) 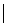 x
x  и
и  }.
}.
Пример. Пусть X ={1,2}, Y ={3,4,5}. Тогда 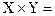 {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)},
{(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)}, 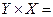 {(3,1), (3,2), (4,1), (4,2), (5,1), (5,2)},
{(3,1), (3,2), (4,1), (4,2), (5,1), (5,2)}, 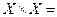 {(1,1), (1,2), (2,1), (2,2)}.
{(1,1), (1,2), (2,1), (2,2)}.
Две пары (x, y) и (u, v) считаются равными тогда и только тогда, когда x = u и y = v
Аналогично можно определить декартово произведение n множеств 
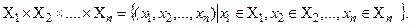
Если  , то n -я степень множества X определяется как
, то n -я степень множества X определяется как 
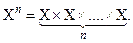
Пример. Множество 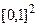 равно множеству
равно множеству
 , которому соответствует множество точек на плоскости, имеющих неотрицательные координаты, не превосходящие единицы (рис. 1.6).
, которому соответствует множество точек на плоскости, имеющих неотрицательные координаты, не превосходящие единицы (рис. 1.6).
 Рис. 1.6
Рис. 1.6
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2697; Нарушение авторских прав?; Мы поможем в написании вашей работы!