Счетные и несчетные множества

Между множествами

Взаимно однозначное соответствие

Иногда бывает необходимо сопоставлять друг с другом элементы некоторых множеств. Рассмотрим, например, два множества: стадо из четырех овец и рощу из четырех деревьев. Эти множества находятся между собой в таком отношении, в каком ни одно из них не находится с кучей из трех камней или с рощей из семи деревьев. Их можно попарно сопоставить друг с другом, привязав овец к де­ревьям, так что каждая овца и каждое дерево будут в точ­ности принадлежать одной и той же паре. Такое соответствие между элементами двух множеств называется взаимно однозначным соответствием.

Пусть X и Y два конечных множества: m - и n -элементные. Между ними можно установить взаимно однозначное соответствие только в том случае, если m = n. Сколько же существует таких взаимно однозначных соответствий для двух n -элементных множеств X и Y? Первый элемент множества X может быть сопоставлен с любым из n эле­ментов множества Y. Для каждого такого сопоставления второй элемент множества X может быть сопоставлен с любым из оставшихся n -1 элементов множества Y и т. д. После того, как такое сопоставление проведено для n -1 элементов множества X, последний элемент этого множества будет сопоставляться с единственным остав­шимся элементом множества Y. Таким образом, общее число взаимно однозначных соответствий для n -элементных множеств будет n (n -1)... 1= n!

Если множества являются бесконечными, то установление между ними взаимно однозначного соответствия наталкивается на трудности, связанные с необходимостью оперировать с бесконечно большим чис­лом элементов множества. За основу для сопоставления бесконечных множеств принято брать натуральный ряд чисел N: 1, 2,.... n...

Если бесконечное множество оказывается возможным привести во взаимно однозначное соответствие с натуральным рядом чисел, то такое множество называют счетным. Следует отметить, что не все бесконечные множества являются счетными. Если бесконечное множество невозможно привести во взаимно однозначное соответствие с натуральным рядом чисел, то его называют несчетным.

В качестве примера бесконечного множе­ства рассмотрим множество равносторонних треугольников, в которых вершинами каждого треугольника являются середины сторон уже построенного треугольника (рис. 1.7). Это бесконечное множество равносторонних тре­угольников можно привести во взаимно одно­значное соответствие с натуральным рядом чисел, расположив их в порядке уменьшения длин сторон, т. е. в виде последовательности T₁, T₂ …, Т_n … Следова­тельно, рассмотренное бесконечное множество равносторонних треуголь­ников является счетным. Однако существует бесконечное множество дру­гих равносторонних треугольников, не входящих в рассмотренное мно­жество. Вопрос о том, является ли счетным множество всех равносто­ронних треугольников или всех треугольников вообще, требует допол­нительного исследования.

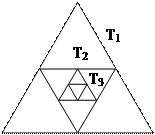
Рис. 1.7. Бесконечное множество

равносторонних треугольников

Приведем несколько примеров счетных множеств.

1. Множество квадратов целых чисел 1, 4, 9,..., n²... представ­ляет собой лишь подмножество множества натуральных чисел N. Одна­ко множество является счетным, так как приводится во взаимно одно­значные соответствия с натуральным рядом путем приписывания каждому элементу номера того числа натурального ряда, квадратом которого он является.

2. Счетным является множество Z всех целых чисел – положи­тельных и отрицательных, хотя натуральный ряд представляет собой лишь подмножество этого множества. Это можно установить, рассмот­рев взаимно однозначное соответствие

N: 1 2 3 4 5 6 7...

Z: 0 1 –1 2 – 2 3 –3...,

из которого следует, что

3. Еще более удивителен тот факт, что счетным оказывается мно­жество всех рациональных чисел, т. е. чисел, которые могут быть представлены в виде дроби r = q / p, где q и p – любые целые числа. Для того чтобы убедиться в этом, представим все множество рацио­нальных чисел в виде следующей таблицы, в которую, естественно, заносим несократимые дроби:

Обходя таблицу по направлению стрелок, приходим к последова­тельности

1, 2, 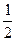, , , 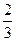3, 4, , , , , , , …,

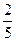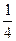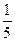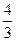позволяющей занумеровать все эти числа.

Из приведенных примеров видно одно из замечательных свойств бесконечных множеств – возможность приведения во взаимно одно­значное соответствие бесконечного множества с его бесконечным же подмножеством, которое не имеет места в случае конечных множеств. Существование несчетных множеств следует из теоремы, доказан­ной немецким математиком Г. Кантором в 1874 г.

Теорема 1.5.1. Множество всех действительных чисел интервала 0< x £1 несчетно.

Заметим, что любое число рассматриваемого интервала представ­ляет собой конечную или бесконечную десятичную дробь вида 0, a₁a₂a₃a₄ … и может быть представ­лено точкой отрезка вещественной оси. Следовательно, теорема утверждает, что множество точек отрезка (0, 1] не­счетно.

Доказательство. Для доказа­тельства предположим, что последова­тельность х₁, х₂, х_з, x₄... представляет собой бесконечный перечень действи­тельных чисел, принадлежащих этому интервалу. Вопрос состоит в том, может или не может подобный перечень содер­жать все числа этого интервала, т. е. нельзя ли найти число, которое принад­лежит этому интервалу, но конечно не входит в указанный пере­чень чисел. Для того, чтобы найти такое число, запишем все входящие в перечень десятичные дроби одну под другой:

Образуем диагональную дробь, указанную стрелками, и заменим в ней каждую из последовательных цифр a_nn на отличную от нее цифру а'_nn так, чтобы при этом не получилась конечная дробь. Полу­ченная дробь 0, a’₁₁a’₂₂a’₃₃a’₄₄ … представляет собой действительное число, принадлежащее нашему интервалу, но не входящее в рассматри­ваемый перечень. Действительно, эта дробь отличается от первой из данных дробей своей первой цифрой после запятой, от второй – своей второй цифрой после запятой, от третьей – третьей цифрой и т. д.

Необычные свойства несчетных множеств проявляются в том, что рассмотренный интервал (0, 1] может быть приведен во взаимно одно­значное соответствие с любым другим интервалом (а, b ]. Такое взаимно однозначное соответствие можно осуществить с помощью централь­ной проекции (рис. 1.8). Таким образом, несчетным является множе­ство всех действительных чисел любого интервала (а, b].

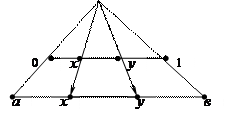Рис. 1.8. Взаимно однозначное соответствие между

интервалами (0, 1] и (а, b ]

Дата добавления: 2014-12-27