Следствие. Следствия из закона Гесса

Следствие

Следствия из закона Гесса.

Тепловой эффект химической реакции при стандартных условиях равен сумме стандартных энтальпий образования продуктов реакции за вычетом суммы стандартных энтальпий образования исходных веществ.

Например:

СН₄(г) + 2О₂(г) = СО₂(г) + 2Н₂О(ж)

∆ Н^ореакции = [∆Н^о_f ,₂₉₈(СО₂) + 2 ∆Н^о_f ,₂₉₈(Н₂О)] - [ ∆Н^о_f ,₂₉₈(СН₄) + 2 ∆Н^о_f ,₂₉₈(О₂)] =

[-393,5 + 2(-241,8)] - [(-74,8) + 2∙ 0] = -802,3 кДж.

Тепловой эффект химической реакции при стандартных условиях равен сумме стандартных энтальпий сгорания исходных веществ за вычетом суммы стандартных энтальпий сгорания продуктов реакции.

Например:

С₂Н₂ (г) + СО(г) + Н₂О(ж) = СН₂ = СН—СООН(ж)

∆ Н^ореакции = [∆Н^о_сг ,₂₉₈(С₂Н₂) + ∆Н^о_сг ,₂₉₈(СО) + ∆Н^о_сг ,₂₉₈(Н₂О) – [ ∆Н^о_сг ,₂₉₈(С₂Н₃СООН)] =

[-1299,6 - 282,5 + O] - [-1370,0] = -211,13 кДж

Первое начало термодинамики не даёт ответа на вопрос о направлении самопроизвольно протекающих процессов при данных условиях. Самопроизвольные процессы—это процессы, происходящие вокруг нас, которые, исходя из опыта, мы считаем наиболее вероятными.

Например: энтальпия реакции 12С(т) + 11Н₂О(ж) = С₁₂Н₂₂О₁₁(т), рассчитанная по закону

Гесса ∆Н<O, хотя она реально неосуществима.

А у реакции N₂(г) + O₂(г) = 2NO(г) ∆Н>O, но она протекает при высокой температуре.

Таким образом, изменение энтальпии нельзя считать единственной причиной самопроизвольного протекания реакций. Существует ещё функция состояния системы, изменение которой оказывает влияние на направление процесса — энтропия S. Энтропия – функция состояния системы, величина которой показывает меру неупорядоченности хаотичности системы.

Одна из формулировок второго начала термодинамики— в изолированных системах самопроизвольно протекающие процессы сопровождаются увеличением энтропии.

Для необратимых процессов в изолированных системах изменение энтропии ∆S>O,

для обратимых процессов ∆S = O. Все реальные процессы необратимы, лишь небольшое число из них можно приближённо рассматривать как обратимые. Следовательно, в результате реальных процессов энтропия изолированной системы всегда увеличивается.

Чем ближе термодинамическое равновесие тем больше хаотичность расположения молекул в теле или в системе. Следовательно самопроизвольные процессы в изолированных системах протекают только в направлении возрастания энтропии S.

∆S = S₂ - S₁ >O идёт процесс 1→ 2

∆S = S₂ - S₁ <O идёт процесс 2 ← 1

∆S = O термодинамическое равновесие

В неизолированной системе самопроизвольно протекают реакции, в результате которых химическая система достигает состояния, характеризующегося не только меньшей энтальпией, но и большей энтропией.

Учесть одновременно оба фактора для систем находящихся при постоянном давлении и температуре позволяет функция состояния — свободная энергия Гиббса: G = H —TS.

Абсолютные значения энергии Гиббса, так же как и абсолютные значения энтальпии, невозможно определить, поэтому используют уравнение ∆G =∆ H —T∆S

Условием самопроизвольного протекания изобарно-изотермических процессов является неравенство ∆G<O. Реакция продолжается до достижения минимального значения энергии Гиббса. В обратимых реакциях минимальная энергия системы достигается в состоянии химического равновесия. После установления химического равновесия ∆G = O.

Величина энергии Гиббса складывается из энтальпийного вклада ∆H и энтропийного вклада T∆S.

Рассмотрим различные варианты:

1. ∆H<O, ∆S >O ∆G <O процесс протекает в прямом направлении независимо от величин ∆H,∆S,T

2 ∆H <O, ∆S <O ∆G <O, если |∆H|>|T∆S|, такие реакции возможны при низких температурах

3. ∆H >O, ∆S <O ∆G >O, процесс может протекать только в обратном направлении

4. ∆H > O,∆S >O∆G<O, если |T∆S|> |∆H|, процесс может протекать при высокой температуре

Равновесное состояние — термодинамическое состояние сиcтемы, которое при постоянных внешних условиях не изменяется во времени, причём стабильность характеристик системы (состав, давление и др.) не обусловлена протеканием какого-либо внешнего процесса.

Признаки истинного равновесия системы:

1. Неизменность равновесного состояния системы при сохранении внешних условий.

2. Подвижность равновесия —самопроизвольное восстановление равновесие после прекращения внешнего воздействия.

3. Динамический характер равновесия— скорость прямого процесса равна скорости обратного процесса.

4. Состояние системы будет одинаковым независимо от того, с какой стороны она подходит к равновесию.

5. Энергия Гиббса в состоянии истинного термодинамического равновесия минимальна Gmin,

a изменение энергии Гиббса равно нулю ∆G=0.

Концентрации реагентов и продуктов реакции в состоянии химического равновесия называются равновесными.

Состояние равновесной химической системы характеризуется по закону действующих масс константой равновесия.

Для обратимой химической реакцией, которую в общем виде можно изобразить уравнением:

aA + bB = dD + qQ константа равновесия имеет вид:

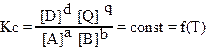
где Кс — константа равновесия; [A], [B] — равновесные концентрации исходных веществ;

[D], [Q] — равновесные концентрации продуктов реакции; a,b,d,q — стехиометрические коэффициенты.

Выражение константы равновесия показывает: для идеальных систем в состоянии химического равновесия отношение произведений концентраций продуктов реакции в степенях, равных стехиометрическим коэффициентам, к произведению концентраций исходных веществ в степенях, равных стехиометрическим коэффициентам, есть величина постоянная при данных температуре давлении и в данном растворителе.

В общем случае формулировка закона действующих масс гласит: в состоянии химического равновесия отношении произведений активностей продуктов реакции в степенях, равных стехиометрическим коэффициентам, к произведению активностей исходных веществ в степенях, равных стехиометрическим коэффициентам, есть величина постоянная при данных температуре давлении и в данном растворителе.

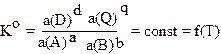
Факторы, влияющие на величину константы химического равновесия:

1.Природа реагирующих веществ 2.Температура.

Факторы не влияющие на величину константы равновесия:

1. Концентрации реагирующих веществ
2. Давление в реакционной системе
3. Наличие примесей

Дата добавления: 2014-12-27