Тема лекции 11. Статистическое изучение взаимосвязи социально-экономических явлений

Конспект лекции: Как правило, вычисления в социально-экономических исследованиях проводятся на основе ограниченного числа данных, ко­торые можно рассматривать как выборочные. Поэтому, естественно, возникает вопрос о вероятностной оценке полученных данных, а именно о значимости полученных результатов корреляционного и регрессионного анали­за.

Простейшей системой корреляционной связи является линейная связь между двумя признаками — парная линейная корреляция. Уравнение парной линейной корреляционной связи на­зывается уравнением парной регрессии и имеет вид:

Уравнение парной линейной регрессии имеет вид:

(36)

где — среднее значение результативного признака у при определен­ном значении факторного признака х;

а — свободный член уравнения;

b — коэффициент регрессии, измеряющий среднее отношение от­клонения результативного признака от его средней величины к отклонению факторного признака (от его средней величины на одну единицу его измерения), — вариация у, приходящаяся на единицу вариации х.

Параметры уравнения (36) рассчитываются методом наи­меньших квадратов (МНК) по данным о значениях признаков х и у в изучаемой совокупности, состоящей из n единиц.

Исходное условие МНК для прямой линии имеет вид:

(37)

Для отыскания значений параметров а и b, при которых f(а, b) принимает минимальное значение, частные производ­ные функции приравниваем нулю и преобразуем полученные уравнения, которые называются нормальными уравнениями МНК для прямой:

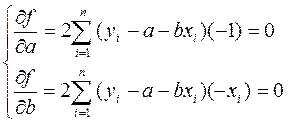(38)

Отсюда система нормальных уравнений имеет вид:

(39)

Нормальные уравнения (МНК) для прямой линии регрес­сии являются системой двух уравнений с двумя неизвестны­ми a и b. Все остальные величины, входящие в систему, оп­ределяются по исходной информации. Таким образом, оба параметра уравнения линейной регрессии однозначно вычис­ляются при решении этой системы уравнений.

Если первое нормальное уравнение разделить на n, полу­чим

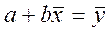, откуда (40)

По уравнению (35) обычно на практике вычисляется сво­бодный член уравнения регрессии а. Параметр b — коэффициент регрессии вычисляется по преобразованной формуле, которую можно вывести, решая систему нормальных уравнений относительно b:

(41)

Так как знаменатель этого выражения есть не что иное, как дисперсия признака, т.е. а_х, то можно записать формулу коэффициента регрессии в виде

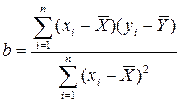, или (42)

где в числителе ковариация переменных.

При оценке могут быть подвергнуты показатели тесноты связи изучаемых признаков, параметры полученного корреляционного уравнения, точ­ность аппроксимации, индивидуальные значения теоретического уровня признака и, наконец, уравнение корреляции в целом. Оценка вышепере­численных результатов корреляционного анализа производится с приме­нением распределения Стьюдента и распределения Фишера - Снедекора. Рассмотрим статистическую оценку некоторых результатов корре­ляционного анализа для линейной зависимости.

Значение коэффициента парной корреляции является случайной ве­личиной, изменяющейся от выборки к выборке. Оценку «истинного» коэффициента корреляции в генеральной совокупности р, который ха­рактеризует «истинную» тесноту связи явлений в генеральной сово­купности, можно произвести с помощью построения доверительного интервала:

(43)

где — среднеквадратическая ошибка выборочного парного коэффици­ента корреляции:

(44)

Здесь n — число наблюдений.

Величина r (табличное значение) имеет распределение t- Стьюдента с числом степеней свободы, равным n - 2, уровень значимости а опреде­ляется как единица минус принятая величина вероятности.

Если мы хотим определить значимость отличия r от р, то при уровне значимости а проверяем нулевую гипотезу Н_o (о равенстве нулю р): р = 0. Для этого вычислим наблюдаемое значение критерия:

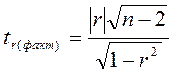(45)

и сравним его с табличным. При этом если:

♦ - нет оснований отвергать нулевую гипотезу;

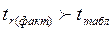♦ - нулевую гипотезу отвергают.

При небольшом числе наблюдений в выборке и при высоком коффициенте корреляции (> 0,9) для построения доверительного интервала и проверки значимости используют преобразование Фишера:

(46)

Наблюдаемое значение критерия определяют как

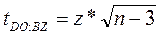(47)

и сравнивают с теоретическим t _та6л (интеграл вероятностей).

Значимость полученной величины коэффициента регрессии а₁ в выборочном теоретическом уравнении у проверяется аналогично зна­чимости коэффициента корреляции r. Среднеквадратическая ошибка равна:

(48)

Для проверки нулевой гипотезы вычисляем наблюдаемое значение критерия:

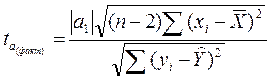(49)

и сравниваем с табличным распределением Стьюдента при избранном уровне значимости а.

Доверительные интервалы для индивидуальных значений 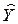при при­нятой вероятности определяются так:

(50)

Графически приведенное выражение — это две симметричные пря­мые, параллельные линии регрессии.

Остаточная дисперсия , т. е. та часть дисперсии зависимой пере­менной, которая не объясняется влиянием рассматриваемого фактора X определяется следующим образом:

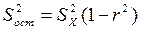(51)

где r ² — коэффициент детерминации (показывает долю дисперсии у, объясняемую аргументом х).

Остаточная дисперсия может быть также определена по формуле:

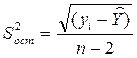(52)

Проверку значимости найденной зависимости можно произвести с помощью распределения Фишера—Снедекора:

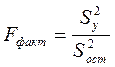(53)

Полученное значение сравнивается с табличным при избранном уровне значимости и соответствующем числе степеней свободы (n -1-для большей дисперсии n -3- для меньшей дисперсии). Если оно окажется больше табличного, то гипотеза о том, что выравнивание по уравнению корреляции хуже, чем по уравнению , отвергается.

Для оценки адекватности можно также воспользоваться показателем средней ошибки аппроксимации:

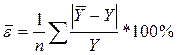(54)

Исследователь сам задает величину средней ошибки. Обычно в соци­ально-экономических исследованиях считается приемлемым .

Конспект лекции:

Основная литература 1 [ 320-391], 4 [ 98-110].

Контрольные вопросы:

1. Распределение t- Стьюдента.

2. Проверка нулевой гипотезы.

3. Доверительные интервалы для индивидуальных значений

4. Формула остаточной дисперсии

5. Показатели средней ошибки аппроксимации:

Дата добавления: 2014-12-23