Тема лекции 9. Методы анализа тенденции в рядах динамики

Конспект лекции: Моделирование основной тенденции (тренда) временных динамических рядов связаны с случайным соци­ально-экономическим процессом. При этом разбить на систематическую составля­ющую, которая является детерминированной и связанной с ходом вре­мени t, и случайную компоненту ε _t - остаток, т. е.:

Y_t=ƒ(t)+ε_t (22)

Первое слагаемое отражает некоторое общее направление развития общественных явлений их основную тенденцию (тренд), второе - действие случайных факторов на уровень экономического явления. Количественное описание тенденции может быть сделано с помощью различных методов.

Метод укрупнения интервалов

Сущность его заключается в том, что с помощью средних величин коле­бания отдельных уровней временного ряда взаимно погашаются и тренд ряда проявляется более отчетливо.

Метод скользящего среднего состоит в нахождении центрированных средних скользящего интервала. Сглаженный ряд короче первоначального на

(К- 1) уровней при ширине избранного интервала К.

Метод аналитического выравнивания состоит в аналитическом выравнивании фактические уровни временного ряда и заменяются теоретическими на основе линейной или нелиней­ной формы связи. В качестве факторного признака принимается время. Таким образом, тенденция временного ряда представляется некоторым уравнением регрессии.

Авторегрессионная модель временного динамического ряда

Авторегрессия первого порядка. Уровни временного динамического ряда - случайные величины, имеющие определенную закономерность распределения во времени. В ряде случаев они не являются независимыми: зачастую во временных рядах наблюдается зависимость последующих уровней яв­ления от предшествующих им во времени. Эта зависимость называется автокорреляцией и может быть оценена коэффициентом автокорреля­ции ρ_t.

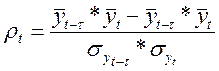(23)

Последовательность коэффициентов автокорреляции между данным временным и этим же рядом, сдвинутым на τ сдвигов (лаги). Зависимость уровня ряда от предыдущих с увеличением сдвига τ.

Зависи­мость одних уровней ряда от других может быть оценена количественно с помощью уравнения авторегрессии.

Парное линейное уравнение авторегрессии (уравнение первого по­рядка) имеет вид:

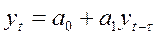(24)

где a ₀, а₁ - параметры уравнения.

Фактическое значение уровня временного ряда может быть пред­ставлено соответственно как:

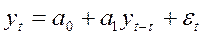(25)

где ε - остаток.

Авторегрессия высших порядков. Если данные автокорреляционной функции свидетельствуют о высокой степени тесноты связи уровней временного ряда нескольких последовательных сдвигов, то для модели­рования данного уровня можно прибегнуть к построению многофактор­ной регрессии. Независимыми факторными признаками в ней будут выступать уровни явления нескольких предыдущих периодов.

Так, уравнение авторегрессии с тремя факторными признаками (3-го порядка) имеет вид:

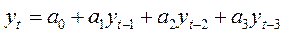(26)

Дата добавления: 2014-12-23