Тема лекции 7. Выборочное наблюдение

Конспект лекции: Выборочное наблюдение - наиболее совершенная разновидность не­сплошного наблюдения, при котором из общей (генеральной совокуп­ности) обследованию подвергается некоторая часть, называемая выбо­рочной совокупностью. Обобщающие показатели, характеризующие эту обследованную часть, распространяются на всю совокупность.

Вы­борочный метод отличается от других видов несплошного наблюдения, во-первых, тем, что заранее устанавливается, сколько единиц или какая часть генеральной совокупности будет обследована, и, во-вторых, зара­нее определяется порядок отбора, при котором выборочная совокуп­ность в достаточной мере репрезентовала бы (представляла) генераль­ную совокупность.

Применение выборочного метода связано с возникновением присущих ему ошибок репрезентативности, которые представляют собой разность между генеральными и выборочными обобщающими показателями.

Существуют различные способы отбора единиц исследуемой генераль­ной совокупности в целях образования выборочной. Их классифика­ция представлена на рисунке 1. Рассмотрим различные способы отбора единиц генеральной совокуп­ности, представленные на рисунке 6.

Индивидуальный отбор - выборочная совокупность образуется при последовательном отборе отдельных единиц.

При серийном отборе формирование выборочной совокупности производится сериями.

Вы­борку, при которой отбор производится непреднамеренно, случайно, называют случайной, если же механически через равный интервал - механической.

Типический отбор предполагает предварительное деление генеральной совокупности на однородные группы, а затем отбор из образованных групп одним из рассмотренных выше способов.

Повтор­ный отбор предполагает возвращение перед очередным отбором обсле­дованной единицы или серии в генеральную совокупность, бесповтор­ный отбор такого возвращения не предусматривает.

Особой разновидностью выборочного наблюдения является моментно-выборочное наблюдение. Оно состоит в фиксации наличия отдель­ных элементов изучаемого процесса на определенные моменты времени без учета длительности данного элемента.

С точки зрения оценки репрезентативности выборочных обобщаю­щих показателей различают большие и малые выборки.

Будем считать выборку безусловно большой, если численность единиц в ней превыша­ет 100, и безусловно малой, если численность единиц в ней меньше 20.

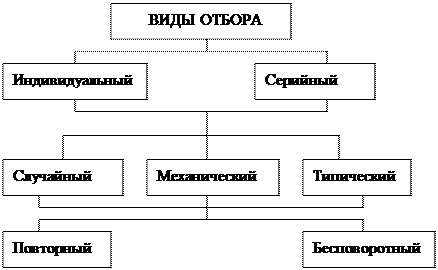
Рисунок 6. Виды отбора выборочного наблюдения

Определение объема и ошибок большой выборки

Определение ошибок и объема выборки покажем применительно к слу­чайному бесповоротному отбору, так как последний чаще всего имеет место в социально-экономических исследованиях.

При случайном отбо­ре выборочная средняя 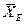,как и выборочная доля ω, является перемен­ной величиной при различных исходах выборки и колеблется около со­ответствующих генеральных значений средней 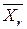и доли p.

Мерой этой колеблемости является стандартная ошибка средней 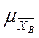и доли :

(14)

где п - объем выборки;

N - объем генеральной совокупности;

s² - выборочная дисперсия.

Предельная ошибка выборки может быть определена для средней как:

,

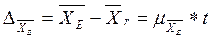адля доли как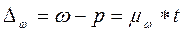

(где р - генеральная доля). Коэффициент t зависит от вероятности, с которой можно гарантировать, что предельная ошибка выборки не пре­высит t -кратную стандартную ошибку.

Значения t для различных веро­ятностей (интеграл вероятностей) табулированы. Объем выборки для определения средней:

(15)

и для определения доли

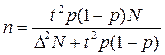
(16)

Определение объема и ошибок малой выборки

В практике социально-экономических исследований часто приходится пользоваться малыми выборками. При малых выборках методы оценок параметров генеральной совокупности, разработанные применительно к нормальному распределению, нуждаются в корректировке. Так, стан­дартная ошибка средней имеет вид:

(17)

а взаимосвязь t и вероятности для расчета предельной ошибки определяются в этом случае распределением Стьюдента, значения которого также табулированы. Определение объема малой выборки производится таким же способом, что и большой, но с использованием указанного распределения.

Основная литература 2 [114-268], 4 [73-88],

Дополнительная литература 1[ 46-70].

Контрольные вопросы:

1. Вы­борочный метод

2. Виды отбора выборочного наблюдения

3. Предельная ошибка доли

4. Предельная ошибка выборки

5.Вид стан­дартной ошибки среднего

Дата добавления: 2014-12-23