Тема лекции 5. Средние величины

Конспект лекции: Объект статистики как общественной науки во многом специ­фичен, в известном смысле формы величины и мето­ды познания показателей. Изучение разнообразных форм стати­стических показателей со стороны величины (средние, показа­тели структуры, индексы и т. д.) с учетом специфики явлений жизни общества осуществляет общая теория статистики. Она со­средоточивает внимание на общих свойствах статистических пока­зателей и составляющих их элементов, на общих методах и прие­мах получения (познания) объективных показателей.

Изучение многообразия объективных статистических показа­телей по содержанию (включая все богатство форм содержания) в связи с их количественной стороной выполняет социально-эко­номическая статистика со всеми своими отраслевыми подразделе­ниями. Общество и рыночная экономика представляют собой весь­ма сложную систему, имеют много взаимосвязанных существен­ных сторон и отношений. Адекватная изучаемому объекту диффе ренциация его особых, являющихся предметом статистики признаковпо содержанию) означает систему признаков, систему пока­зателей. Следовательно, социально-экономическая статистика рассматривает систему, объективных статистических показателей состояния и развития общества, состояния и развития экономики.

Среди обобщающих показателей, которыми статистика характеризует общественные явления, большую роль играют среднее величины.

Средней величиной в статистике называют обобщающую характеристику совокупности однородных общественных явлении, которая показывает типичный уровень варьирующего признака в расчете на единицу совокупности. Она обобщает многие индивидуальные величины одного и того же вида. Вид среднего в статистике подчинен социально-экономическому содержанию изучаемых явлений. Соотношения, выражающие смысл средних, называют исходными соотношениями. Они являются базой расчета и критерием правильности выбора вида средней в статистике. Часто применяются средняя арифметическая. Например: Средний срок службы станков = Суммарный срок службы всех станков / Общее количество станков.

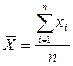(1)

Виды средних величин. Средние, используемые в статистике, делятся на два класса: степен­ные средние и структурные средние. Из первого класса наиболее часто применяются средняя арифметическая и средняя гармоническая. Сред­няя геометрическая применяется только при исчислении средних пока­зателей рядов динамики, средняя квадратическая — при исчислении показателей вариации.

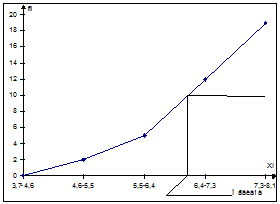
Рисунок 3. Кривая распределения средних величин

Представителями второго класса средних явля­ются мода и медиана.

Средняя ариф­метическая. Для сгруппированных данных средней ариф­метической :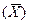

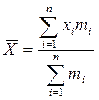(2)

где х_i - варианты признака; т_i - частоты (частости), i=1,2,…,n

Пример расчета средней арифметической и средней гармонической

Таблица 5

Группы станков по срокам службы, х	Число станков в группе mi	Общий срок службы станков по данной группе М=хm
0-5		65,0
5-10		180,0
10-15		225,0
15-20		245,0
20-25		360,0
Всего		1100,0

Если мы располагаем данными, приведенными в графах 1 и 2 табл.5, то исходное соотношение приводит к расчету средней арифметической:

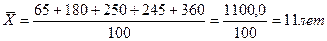
Средняя гармоническая 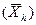: 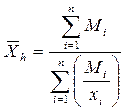(3)

где М_i - суммарный объем i - признаков в данной группе.

Если мы располагаем данными, приведенными в графах 1 и 3 табл.5, то исходное соотношение приводит к расчету средней гармонической:

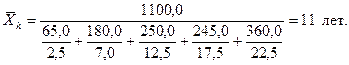
Модой в статистике называют значение признака в данной совокупно­сти, имеющего наибольшую частоту. Значение моды для дискретного вариационного ряда может быть найдено непосредственно. Для интервального вариацион­ного ряда значение моды Мо определяется по следующей формуле

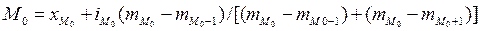(4)

где х_Мо - нижняя граница модального интервала;

i_Mo - величина модального интервала;

m_Mo, m_Mo-1, m_Mo+1 частота модального, предмодального и послемодального интервалов соответственно.

Приведенная формула (3) моды может быть использована в ва­риационных рядах с равными интервалами на рисунке 3 и расчеты соответственно.

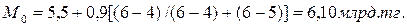
Медианой в статистике называют признак, делящий численность вариационного ряда по сумме накопленных частот на две равные части. Для нахождения медианы Ме в интервальном вариационном ряду применяют следующую формулу:

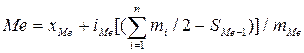(5)

где Σm - сумма частот вариационного ряда; S_Me-1 - сумма накопленных частот до медианного интервала.

Для примера таблицы 5 медиана равно 10 лет.

Дополнительно к медиане для характеристики структуры вариационного ряда исчисля­ют квартили и процентили, которые ряд делят по сумме частот соответ­ственно на четыре и на сто равных частей.

Средняя величина признака не позволяет судить о тех колебаниях, ко­торым подвержен изучаемый признак в данной совокупности. Для оп­ределения величины этой колеблемости в статистике применяют пока­затели вариации.

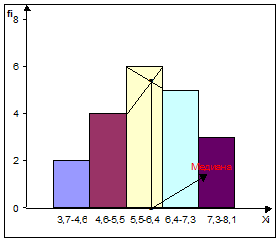Медиану и моду можно определить графически. Медиана определяется по кумуляте. Для ее определения вы­соту наибольшей ординаты, которая соответствует общей числен­ности совокупности, делят пополам. Через полученную точку про­водят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Рисунок 4. Полигон распределения группированных модальных данных

Мода также определяется по гистограмме распределения (рисунок 4.). Для это­го правую вершину модального прямоугольника соединяем с пра­вым верхним углом предыдущего прямоугольника, а левую вер­шину модального прямоугольника - с левым верхним углом по­следующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Основной характеристикой центра распределения является средняя арифметическая, опирающаяся на всю информацию об изучаемой совокупности единиц. Однако в ряде случаев средняя арифметическая должна быть дополнена и даже заменена модаль­ным значением или медианой.

Например, в статистическом конт­роле качества продукции удобнее пользоваться медианой, а не средней арифметической, так как определение медианы для ран­жированного ряда данных не требует специального расчета. Кро­ме того, она не чувствительна к крайним значениям взятой конт­рольной пробы. В рядах с открытыми интервалами также целе­сообразнее пользоваться в качестве характеристики центра рас­пределения модой и медианой. Мода применяется при изучении спроса населения на товары народного потребления (например, на обувь, одежду и т.д.), когда интерес представляет определение модального размера, т.е. размера, пользующегося наибольшим спросом.

Основная литература: 1[121-169], 4 [20-29].

Контрольные вопросы:

1. Значение моды для дискретного вариационного ряда;

2. Величина модального интервала для ряда

3. Средние величины в статистике

4. Назовите виды средних величин.

5. Общая характеристика структурного ряда

Дата добавления: 2014-12-23