Тема лекции 10. Индекы

Конспект лекции: Статистическим индексом называют обобщающий относительный показатель сравнения двух совокупностей, состоящих из элементов, непос-редственно не поддающихся суммированию, например совокупность, где элементами выступают хлопок и станки. Наиболее распространена сравнительная характеристика совокупностей во времени. Здесь индексы выступают как временные показатели (показатели динамики). Индексный метод применяется также в статистике как аналитическое орудие - для оценки роли отдельных факторов в изменении сложного явления. Классификация индексов представлена на рис. 9.

К индексам объемных показателей относятся индексы физического объема продукции, физического объема товарооборота, физического объема валового национального дохода и т. д.

Индексы качественных показателей включают в себя индексы цен, себестоимости, производительности труда и др.

Общие индексы характеризуют изменение совокупности в целом, например валовой продукции народного хозяйства в отчетном году по сравнению с предыдущим.

Индивидуальные индексы дают сравнительную характеристику динамики отдельных элементов совокупности, например выпуска чугуна в двух периодах.

Групповые индексы характеризуют динамику не всей совокупности, а только ее части, например индекс валовой продукции машиностроительной отрасли. Агрегатные и средние из индивидуальных индексов определяются методологией их расчета. Если база для сравнения всех уровней явления остается постоянной, получаемый индекс называют базисным, в противном случае — цепным.

Индивидуальный индекс цен

Чтобы получить характеристику изменения цен на какой-либо продукт, рассчитывают индекс:

где 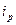- индивидуальный индекс цен;

р₁, р₀— цена единицы продукта в отчетном и базисном периодах соответственно.

Индивидуальный индекс физического объема продукции

Чтобы получить характеристику изменения количества товара, рассчитывают индекс:

где 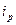- индивидуальный иңдекс физического объема;

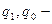количество товара в отчетном и базисном периодах соответственно.

Индексный метод анализа факторов динамики явлений

Индексный метод анализа факторов динамики явлений применяется в тех случаях, когда между результативным и факторными показателями существует функциональная связь. Первым этапом анализа является установление формы связи признаков, затем строится система взаимо­связанных индексов.

Если результативный показатель представляется произведением фак­торов-сомножителей (у = х * z * w), то система взаимосвязанных ин­дексов может быть построена двумя методами:

во-первых, выявлени­ем воздействия каждого фактора при условии, что все остальные не изменяются, т. е. находятся на базисном уровне:

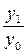=[(x₁z₀w₀)/(x₀z₀w₀)]*[(x₀z₁w₁)/(x₀z₀w₁)]*[(x₀z₀w₁)/(x₀z₀w₀)]

во-вторых, в виде последовательной цепи (цепной метод).

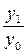=[(x₁z₁w₁)/(x₀z₁w₁)]*[(x₀z₁w₁)/(x₀z₁w₁)]*[(x₀z₀w₁)/(x₀z₀w₀)] (28)

Этот метод требует предварительного обоснования порядка фикси­рования факторов.

Системы взаимосвязанных общих индексов можно подразделить на системы взаимосвязи индексов количественных показателей и систе­мы взаимосвязи индексов средних уровней качественного показателя.

Системы взаимосвязи количественных показателей

Эти системы, аналогично системам индивидуальных индексов, могут быть построены двумя методами. Первый - метод изолированного вли­яния:

Σx₁y₁/∑x₀y₀=[Σx₁y₀/x₀y₀]*[∑x₀y₁/x₀y₀]*[∑x₁y₁/x₀y₁]/[Σx₁y₀/x₀y₀] (29)

где х — качественный признак; у — количественный признак.

Рисунок 9. Классификация индексов

В формуле дополнительный сомножитель в квадратных скобках - индекс ковариации - характеризует степень дополнительного влияния (сверх изолированного изменения х и у), которое является результатом того, что факторы х и у изменялись не изолированно, а во взаимосвязи.

Второй - цепной метод разлагает результативный индекс только на произведение сомножителей-факторов. Например, индекс товарообо­рота может быть разложен так:

∑q₁p₁/Σq₀p₀=(∑p₁q₁/p₀q₁)*(∑q₁p₀/q₀p₀) (30)

В cистеме взаимосвязанных индексов средних уровней качественного показателя (индекс переменного состава I_{перем.сред}) выступает как произведение двух индексов: индекса пока­зателя в неизменной структуре (индекс постоянного состава 1_{пост. сред}) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов I _{струк. сдвиг}):

I_{перем.сред}=I_{пост. сред}* I _{струк. сдвиг}

Агрегатный индекс цен

Чтобы получить сведения об изменении цен на все продукты в виде единого показателя, необходимо сопоставить цены при помощи неиз­менного количества товаров. Такой подход приводит к построению двух равноправных индексов цен:

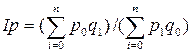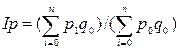1). 2). (31)

где I_p - общий индекс цен.

В статистике в основном применяется первый индекс, так как он дает возможность узнать, как изменился уровень цен на товарную массу, про­изведенную в отчетном году. Разность между числителем и знаменате­лем индекса позволяет получить абсолютную экономию или перерас­ход от изменения цен.

Агрегатный индекс физического объема продукции и товарооборота

Для того чтобы получить сведения об изменении количества различ­ных продуктов в виде единого показателя, необходимо их соизме­рить при помощи неизменного уровня цен. Такой подход приводит к построению двух равноправных индексов физического объема про­дукции:

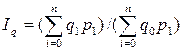1). 2). (32)

где I_p - общий индекс физического объема продукции.

В статистике в основном используют первый индекс, позволяю­щий устранить влияние изменения цен на величину индекса. Раз­ность между числителем и знаменателем индекса дает возможность получить абсолютную величину прироста или падения количества продукции.

Агрегатный индекс физического объема товарооборота строится как отношение стоимости количества продукции отчетного периода в от­четных ценах к стоимости базисного количества продукции в базисных ценах, т. е.:

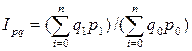(33)

где I _pq - индекс физического объема товарооборота.

Средние индексы из индивидуальных

Если исходные данные не позволяют исчислить общий индекс в агре­гатной форме, прибегают к построению среднего индекса из индиви­дуальных. Критерием правильности построения среднего индекса яв­ляется его равенство агрегатному. При исчислении средних индексов используются только две формы средних: средняя арифметическая и средняя гармоническая.

Средний арифметический индекс может быть получен при помощи преобразования агрегатного индекса физического объема продукции (q₁ =i_qq₀):

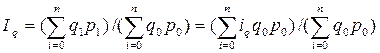(34)

Весами индивидуальных индексов являются слагаемые знаменателя агрегатного индекса.

Средний гармонический индекс может быть получен преобразовани­ем агрегатного индекса цен (p₀ =p ₁/ i_p)

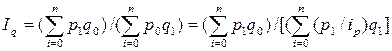(35)

Весами индивидуальных индексов являются слагаемые числителя агрегатного индекса. Этот дополнительный не­изменный показатель выступает в виде индексе в статистическом анализе. Чтобы получить сведения об изменении цен на все продукты в виде единого показателя, необходимо сопоставить цены при помощи неиз­менного количества товаров. Такой подход приводит к построению двух равноправных индексов цен:

Основная литература 1 [520-598], 4 [65-98],

Контрольные вопросы:

1.Сущность системы взаимосвязанных ин­дексов

2. Влияния индекса на изменения структуры цен.

3. Зависимости агрегатного индекса цен от товарооборота.

4. Какой индекс в статистике в основном применяется?

5. Формула среднего арифметического индекса

Дата добавления: 2014-12-23