Геометрическая интерпретация

Рассмотрим геометрическую интерпретацию в случае двух переменных. Этот случай не имеет большого практического значения, но позволяет наглядно представить решение задачи линейного программирования. Разберем пример о производстве красок, рассмотренный ранее.

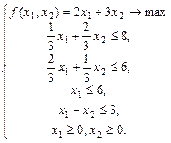
Построим множество допустимых планов X. Для этого найдем множество точек на плоскости, удовлетворяющих первому ограничению. Это будет полуплоскость, лежащая по одну сторону от прямой

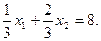
Для того, чтобы определить, по какую сторону от прямой лежит нужное множество, достаточно проверить в одной точке, не лежащей на прямой, выполняется ли в ней нужное неравенство. Возьмем, например, точку (0;0) и подставим ее в первое неравенство:

0 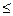8.

Неравенство является верным, следовательно, полуплоскость, удовлетворяющая первому неравенству, лежит по ту же сторону прямой линии, что и точка (0;0). Аналогично построим множества для каждого из ограничений. Множество допустимых планов X получим как пересечение всех этих множеств.

Рис.1

E

А F G

Это будет многоугольник ABCDEF. Затем проводим линию уровня целевой функции LG и параллельно сдвигаем ее в направлении вектора градиента gradf(x) = (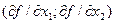 =(2;3) до последнего касания с множеством X. Это касание происходит в точке C, являющейся точкой пересечения прямых лини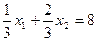й

и . Точкой пересечения этих прямых линий будет точка (4; 10). Таким образом, ежедневно нужно производить 4т краски K ₁ и 10т краски K ₂. Выручка от продажи этой краски составит 38д.ед.

Дата добавления: 2014-12-27