Метод замкнутых контуров

ИССЛЕДОВАНИЕ КИНЕМАТИКИ МЕХАНИЗМА АНАЛИТИЧЕСКИМ МЕТОДОМ.

2.1 Замкнутый контур для механизма II класса.

В плоскости нашего механизма введем координатную систему xy с началом в шарнире О. Звенья 1 и 3 заменим соответственно векторам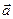и и 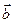. Ползун 2 заменим точкой Е, положение которой задаем двумя векторам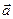и и 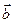.Точку О1 заменим точкой В.ОВ заменим вектором 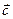,направленным против оси х. Полученный векторный многоугольник показан на рис.2.1.

Рисунок 2.1 – Замкнутый контур для исследуемого механизма

2.2 Характеристика векторов, образующих замкнутый контур механизма.

Вектор 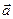изменяется по модулю при движении механизма и является неизвестной функцией времени. Направление этого вектора задано углом .

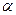Вектор 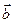не изменяется по модулю (длине) в процессе движения механизма. Модуль этого вектора равен длине ВЕ. Угол b, который определяет положение вектора 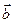, изменяется при движении механизма по известному закону .

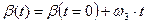Вектор 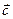не изменяется в процессе движения механизма. Его модуль равен заданному расстоянию ОВ. Направление этого вектора задано углом γ.

2.3 Векторное уравнение замкнутости контура механизма.

Условие замкнутости введенного контура механизма имеет вид

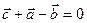. (2.1)

2.4 Проекции векторного уравнения замкнутости контура на координатные оси x и у.

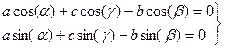. (2.2)

2.5 Решение системы двух уравнений эквивалентной векторному условию замкнутости контура механизма.

Решаем систему (2.2) относительно неизвестных a и β соответственно.

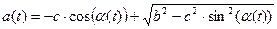, (2.4)

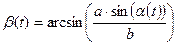. (2.5)

2.6 Угловая скорость звена 3 и проекция скорости точки E ползуна 2 на ось x определим путем дифференцирования по времени t зависимостей (2.6) и (2.7) соответственно.

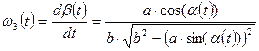. (2.8)

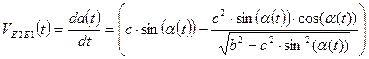. (2.9)

Формулы (2.8) и (2.9) получены с помощью программы, подготовленной для системы программирования MATLAB.

2.7 Угловое ускорение звена 3 и проекция ускорения точки E ползуна 2 на ось x находим дифференцированием по времени t зависимостей (2.8) и (2.9) соответственно.

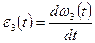. (2.10)

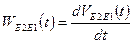. (2.11)

Выражения (2.10) и (2.11) получены с помощью программы и здесь не приводятся в силу их громоздкости. Они приводятся в распечатке работы вышеотмеченной программы.

2.8 Графики временных зависимостей основных кинематических параметров движения механизма.

2.9 Звено 1 – кривошип ОE, вращается равномерно против хода часовой стрелки. Модули скорости и ускорения точки E равны

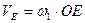=473.6 мм/с, 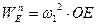=3923 мм/с²

На рис.2.1 и рис.2.2 приведены графики кинематических параметров углового движения звена 3 и поступательного движения звена 2. Графики выведены на временном интервале, соответствующем длительности T1 одного оборота звена 1. Длительность одного оборота звена 1 равна T1=60/n₁=0.75c.

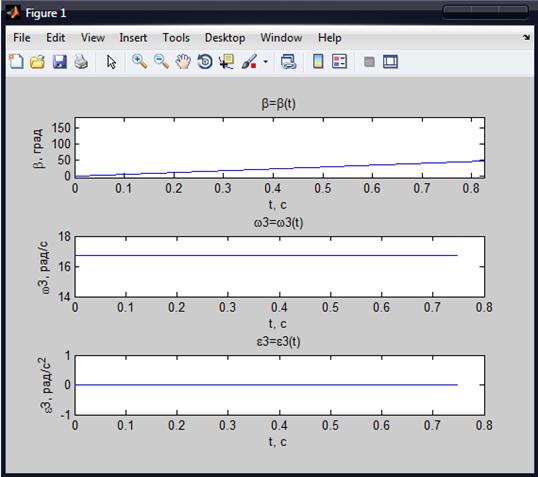
Рисунок 2.1 – Кинематические параметры углового движения звена 3

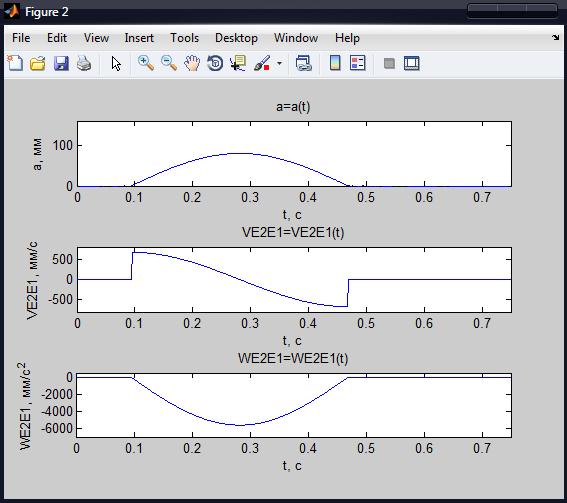
Рисунок 2.2 – Кинематические параметры поступательного движения звена 2

Дата добавления: 2014-12-27