
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод планов скоростей и ускорений
|
|
|
|
ВЕКТОРНО-ГРАФИЧЕСКИМ МЕТОДОМ.
ИССЛЕДОВАНИЕ КИНЕМАТИКИ МЕХАНИЗМА
3.1 Строим план положення механизма для заданного момента времени t0=0,3 с.
На рис.3.1 показан план положения механизма, звенья которого изображены в линейном масштабе kl=1 мм/мм.
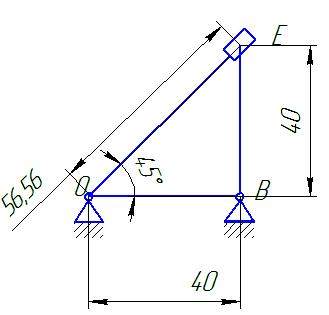
Рисунок 3.1 – План положения механизма для заданного момента времени
3.2 Строим для заданного положения механизма план скоростей.
Рассмотрим соотношения между скоростями крайних точек и средней точки нашей группы Ассура.
Точки E2 (первая крайняя точка) и E3 (средняя точка) принадлежат одному звену 2. Поэтому записываем следующее соотношение
 . (3.1)
. (3.1)
Точки B3 (вторая крайняя точка) и E3 (средняя точка) принадлежат разным звеньям. Для этого случая записываем такое соотношение
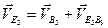 . (3.2)
. (3.2)
Приравняв правые части соотношений (3.1) и (3.2) друг к другу, получим следующее разрешающее векторное уравнение для скоростей
 . (3.3)
. (3.3)
В уравнении (3.3) известны: вектор скорости  ; вектор скорости
; вектор скорости  . Причем
. Причем  =0.
=0.
В уравнении (3.3) имеем два вектора с известными направлениями, но с неизвестными модулями.
Уравнение (3.3) решаем графическим методом путем построения плана скоростей.
На рис.3.2 приведен план скоростей, построенный для заданного положения механизма. Здесь сплошной линией изображен известный вектор скорости  , а штриховыми линиями изображены неизвестные вектора
, а штриховыми линиями изображены неизвестные вектора  и
и  . Точка пересечения этих линий определяет решение уравнения (3.3).
. Точка пересечения этих линий определяет решение уравнения (3.3).
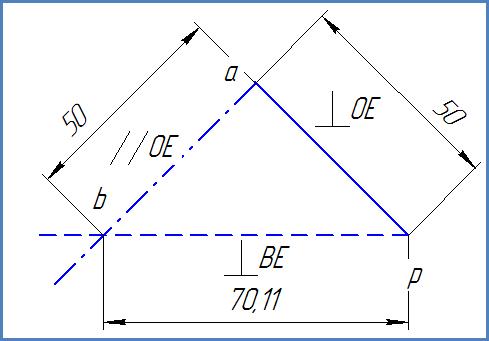
Рисунок 3.2 – План скоростей
Вектор скорости  точки E изображен отрезком
точки E изображен отрезком 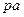 =50 мм. Модуль скорости
=50 мм. Модуль скорости  равен
равен  =473.6 мм/с.
=473.6 мм/с.
Масштабный коэффициент плана скоростей находим по формуле kv = 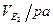 =9.472 мм/с мм.
=9.472 мм/с мм.
Модуль вектора скорости  определяем по формуле
определяем по формуле  =108.284 мм/с.
=108.284 мм/с.
Модуль вектора скорости  определяем по формуле
определяем по формуле 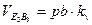 =661,79 мм/с.
=661,79 мм/с.
Итак, линейные скорости всех характерных точек механизма определены.
Угловую скорость  звена 3 находим по формуле
звена 3 находим по формуле  =16,75 рад/с. По направлению вектора скорости
=16,75 рад/с. По направлению вектора скорости  находим, что звено 3 вращается по ходу часовой стрелки.
находим, что звено 3 вращается по ходу часовой стрелки.
Угловая скорость звена 2 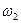 =0, так как это звено движется поступательно.
=0, так как это звено движется поступательно.
Итак, найдены значения и направления угловых скоростей всех звеньев.
3.3 Строим для заданного положения механизма план ускорений.
Рассмотрим соотношения между ускорениями крайних точек и средней точки нашей группы Ассура.
Точки E2 (первая крайняя точка) и E3 (средняя точка) принадлежат одному звену 2. Поэтому записываем следующее соотношение
 . (3.4)
. (3.4)
Точки E2 (вторая крайняя точка) и E3 (средняя точка) принадлежат разным звеньям. Для этого случая записываем такое соотношение
 . (3.5)
. (3.5)
Приравняв правые части соотношений (3.4) и (3.5) друг к другу, получим следующее разрешающее векторное уравнение для ускорений
 . (3.6)
. (3.6)
В уравнении (3.6) известны: вектор ускорения  ; вектор ускорения
; вектор ускорения 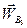 ; вектор ускорения Кориолиса
; вектор ускорения Кориолиса  . Причем
. Причем 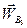 =0,
=0,  =7928 мм/с2
=7928 мм/с2
В уравнении (3.6) имеем два вектора с известными направлениями, но с неизвестными модулями.
Уравнение (3.6) переписываем в следующем виде
 . (3.7)
. (3.7)
Уравнение (3.7) решаем графическим методом путем построения плана ускорений.
На рис.3.3 приведен план ускорений, построенный для заданного положения механизма. Здесь сплошными линиями изображены известные вектора ускорений 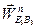 ,
, 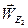 и
и  , а штриховыми линиями изображены неизвестные вектора ускорений
, а штриховыми линиями изображены неизвестные вектора ускорений  и
и 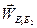 . Точка пересечения этих линий определяет решение уравнения (3.7).
. Точка пересечения этих линий определяет решение уравнения (3.7).
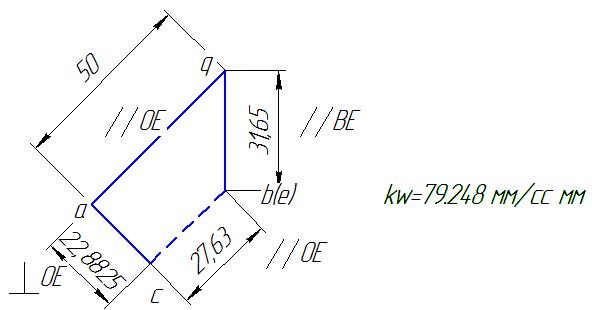
Рисунок 3.3 – План ускорений
Вектор ускорения  точки Е изображен отрезком
точки Е изображен отрезком  =50 мм. Модуль ускорения равен
=50 мм. Модуль ускорения равен 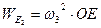 =3962.4 мм/с2.
=3962.4 мм/с2.
Масштабный коэффициент kw плана ускорений находим по формуле kw = 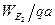 =
=
=79.248 мм/с2 мм.
Длина отрезка 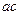 , изображающего ускорение Кориолиса
, изображающего ускорение Кориолиса 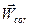 , равна
, равна 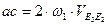 =22.8825 мм.
=22.8825 мм.
Длина отрезка 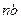 , изображающего тангенциальное ускорение
, изображающего тангенциальное ускорение  , равна 0 мм. Отсюда модуль вектора ускорения
, равна 0 мм. Отсюда модуль вектора ускорения 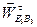 находим по формуле
находим по формуле 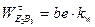 =0 мм/с2.
=0 мм/с2.
Модуль ускорения 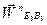 находим по формуле
находим по формуле  =2508.1992мм/с2.
=2508.1992мм/с2.
Модуль ускорения 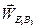 находим по формуле
находим по формуле  =661.8 мм/с2.
=661.8 мм/с2.
Длина отрезка 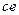 , изображающего ускорение
, изображающего ускорение  , равна 27.63 мм. Отсюда модуль вектора ускорения
, равна 27.63 мм. Отсюда модуль вектора ускорения  определяем по формуле
определяем по формуле  =2189.6 мм/с2.
=2189.6 мм/с2.
Итак, линейные ускорения всех характерных точек механизма определены.
Угловое ускорение 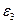 звена 3 находим по формуле
звена 3 находим по формуле  =0 рад/с. По направлению вектора ускорения
=0 рад/с. По направлению вектора ускорения  находим, что угловое ускорение
находим, что угловое ускорение 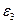 направлено против хода часовой стрелки.
направлено против хода часовой стрелки.
Угловое ускорение звена 2  =0, так как это звено движется поступательно.
=0, так как это звено движется поступательно.
Итак, найдены значения и направления угловых ускорений всех звеньев.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 593; Нарушение авторских прав?; Мы поможем в написании вашей работы!