Множества first и follow

При построении предиктивного синтаксического анализатора необходимо построить два множества связанные с грамматикой G, — FIRST и FOLLOW, которые обеспечивают заполнение таблицы предиктивного анализа грамматики G. Если α — произвольная строка символов грамматики, то определим FIRST(a) как множество терминалов, с которых начинаются строки, выводимые из а. Если а 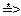λ, то λ входит в FIRST(a).

FOLLOW(A) для нетерминала А определяется как множество терминалов а, которые могут располагаться непосредственно справа от А в некоторой сентенциальной форме, т.е. множество терминалов а, таких, что существуют порождения вида S 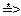αA aβ для некоторых α и β. В процессе приведения между А и а могут появиться символы, но они порождают λ и в конечном счете исчезают. Если А может оказаться крайним справа символом некоторой сентенциальной формы, то $ входит в FOLLOW(A).

FIRST(X) для всех символов грамматики X вычисляетсяс применением следующих правил до тех пор, пока ни к одному из множеств FIRST не смогут быть добавлены ни терминалы, ни λ.

1. Если X — терминал, то FIRST(X)={ X }.

2. Если имеется продукция X → λ, добавим λ к FIRST(X).

3. Если X нетерминал и имеется продукция X → Y₁Y₂...Y_k, то поместим а в FIRST(X), если для некоторого i а є FlRST(Y_i) и λ входит во все множества FIRST(Y₁)… FIRST(Y_i-1), т.е. Y₁ … Y_i-1 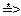λ. Если λ имеется во всех FIRST(Y_i), i = l, k, то добавляем λ к FIRST(X). Например, все, что находится во множестве FIRST(Y_i), есть и в множе­стве FIRST(X). Если Y₁ не порождает λ, то больше мы ничего не добавляем к FIRST(X), но если Y₁ 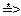λ, то к FIRST(X) добавляем FIRST(Y₂) и т.д.

FIRST для любой строки Х₁Х₂...Х_n вычисляется следующим образом. Добавим к FIRST(Х₁Х₂...Х_n) все не-λ символы из FIRST(X₁). Добавим также все не λ- символы из FIRST(X₂), если λ є FIRST(X₁), все не λ - символы из FIRST(X₃), если λ имеется как в FIRST(X₁), так и в FIRST(X₂) и т.д. И наконец, добавим λ к FIRST(Х₁Х₂...Х_n), если для всех i FIRST(X_i) содержит λ.

FOLLOW(A) для всех нетерминалов А вычисляется с применением следую­щих правил до тех пор, пока ни к одному множеству FOLLOW нельзя будет добавить ни одного символа.

1. Поместим $ в FOLLOW(S), где S — стартовый символ, а $ — правый ограничитель входного потока.

2. Если имеется продукция А → αBβ, то все элементы множества FIRST(β), кроме λ, помещаются в множество FOLLOW(B).

3. Если имеется продукция А → αB, или A → αBβ, где FIRST(β) содержит λ (т.е. β=> λ), то все элементы из множества FOLLOW(A) помещаются в множество FOLLOW(B) [3].

Дата добавления: 2014-12-27