Пример 17

Построение таблиц предиктивного анализа

Пример 16

Для грамматики арифметических выражений

E → TE’

E’ → +TE’| λ

T → FT’

T’ → *FT’| λ

F → (E) | id

множества будут иметь вид:

FIRST(E) = FIRST(T) = FIRST(F) = {(,id}

FIRST(E’) = {+, λ }

FIRST(T’) = {*, λ }

FOLLOW(E) = FOLLOW(E’) = {), $}

FOLLOW(T) = FOLLOW(T’) = {+,), $}

FOLLOW(F) = {+,*,),$}

Например, id и левая скобка добавляются к FIRST(F) по правилу (3) в опреде­лении FIRST, поскольку FIRST(id)={ id }, и к FIRST('(')={(} по правилу (1). По пра­вилу (3) с i =1 из продукции Т → FT' следует, что id и левая скобка входят и в FIRST(T). В соответствии с правилом (2) λ входит в FIRST(E’).

Для вычисления множеств FOLLOW помещаем $ в FOLLOW(E) в соответствии с правилом (1) для вычисления FOLLOW. По правилу (2), примененному к продукции F→(E), правая скобка также входит в множество FOLLOW(E). В соответствии с прави­лом (3), примененным к продукции Е→ТЕ', $ и правая скобка входят в FOLLOW(E'). Поскольку Е' 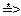λ, эти же символы входят и в FOLLOW(T). Из продукции Е→ТЕ' со­гласно правилу (2), следует, что все, что имеется в множестве FIRST(E’) (за исключением λ), должно входить в множество FOLLOW(T). В это же множество входит также $.

Для построения таблицы предиктивного анализа данной грамматики G используется следующий алгоритм.

1. Для каждой продукции грамматики А → α выполняем шаги 2 и 3.

2. Для каждого терминала α из FIRST(А) добавляем А → α в ячейку М[А, а].

3. Если в FIRST(А) входит λ, для каждого терминала т b из FOLLOW(A) добавим А →b в ячейку М[А, b]. Если λ входит в FIRST(α), а $ — в FOLLOW(A), добавим А → α ячейку М[А, $].

4. Каждая неопределенная ячейка таблицы М указывает на ошибку [3].

Применим алгоритм заполнения таблицы к грамматике из примера 16. Поскольку FIRST(TE’) = FIRST(T) = {(, id } продукция Е → ТЕ' приводит к размещению в ячейках М[Е,(] и M[E, id ] записи E → ТЕ'.

Продукция Е' → + TE' позволяет внести ее в ячейку М[Е',+]. Продукция E' приводит, с учетом FOLLOW(E') = {), $}, к внесению E'→ λ в ячейки М[Е',)] и М[Е',$].

Полностью таблица предиктивного анализа приведена на рис. 29.

Пустые ячейки таблицы означают ошибки; непустые указывают продукции, с помощью которых заменяются нетерминалы на вершине стека.

Нетерминал	Входной символ
id	+	*	(	)	$
E E’ T T’ F	E → TE’ T→FT’ F→id	E’ → +TE’ T’→ λ	T’→*FT’	E→TE’ T→FT’ F→(E)	E’→ λ T’→ λ	E’→ λ T’→ λ

Рис. 29. Таблица разбора для грамматики из примера 16

Стек	Вход	Выход
$E $E’T $E’T’F $E’T’id $E’T’ $E’ $E’T+ $E’T $E’T’F $E’T’id $E’T $E’T’F* $E’T’F $E’T’id $E’T’ $E’ $	id+id*id$ id+id*id$ id+id*id$ id+id*id$ +id*id$ +id*id$ +id*id$ id*id$ id*id$ id*id$ *id$ *id$ id$ id$ $ $ $	E→ TE’ T→FT’ F→ id T’→ε E’→+TE’ E→ FT’ F→ id   T’→ *FT’ F→id T’→ λ E’→ λ

Рис. 30. Перемещения предиктивного синтаксического анализатора при входной строке id+id*id

При входном потоке id+id*id предиктивный синтаксический анализатор осуществляет последовательность перемещений, показанную на рис. 30. Входной указатель при перемещении указывает на крайний слева символ в столбце "Вход". При рассмотрении действий синтаксического анализатора, видно, что его выход совпадает с последовательностью продукций, применяемых в левом порождении. Если же к прочитанным входным символам приписать символы в стеке (от вершины до дна), то получится левосентенциальная форма в порождении.

Синтаксический анализатор находит ошибку в тот момент, когда терминал на вершине стека не соответствует очередному входному символу или на вершине стека находится нетерминал А, очередной входной символ — а, а ячейка таблицы синтаксического анализа М[А, а] пуста.

Дата добавления: 2014-12-27