Дифференциальные уравнения

Реальные объекты не могут мгновенно изменять свое состояние, поэтому вместо статических моделей типа (6.2) для их исследования используют динамические модели, которые описываются дифференциальными уравнениями, содержащими производные (скорости изменения сигналов).

Во многих случаях более или менее точные модели представляют собой нелинейные дифференциальные уравнения, поэтому для того, чтобы применить теорию линейных систем, требуется линеаризация.

Идея линеаризации заключается в том, что в системах регулирования (поддержания заданных значений величин) сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют «правильные» значения и их производные равны нулю. Поэтому для решения задач управления часто достаточно использовать линейную модель в отклонениях от этой рабочей точки.

Модель, только что построенная для бака с жидкостью, не совсем правильная, потому что не учитывает, что уровень в баке изменяется – уменьшается по мере вытекания воды. Кроме того, предположим, что для поддержания уровня используется насос, который подкачивает жидкость в бак, его расход обозначим через Q. Для такого объекта входом является расход Q, а выходом изменение уровня h.

Предположим, что в течение маленького интервала Δ t расходы Q и q можно считать постоянным. За это время объем воды, добавленной в бак насосом, равен Q Δ t, а объем «ушедшей» воды – q Δ t. Учитывая, что площадь сечения бака равна S, получаем изменение уровня 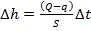. Переходя к пределу при , получаем дифференциальное уравнение

Эта модель учитывает, что уровень жидкости и расходы изменяются во времени. Вспомним, что расход вытекающей жидкости q (t) зависит от уровня воды в баке h (t) и связан с ним нелинейной зависимостью 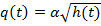. Поэтому уравнение можно записать в виде

(6.6)

Здесь остались только две изменяющиеся величины: расход насоса Q (t) (вход объекта) и уровень воды h (t) (выход). Далее для упрощения записи мы не будем явно указывать зависимость этих сигналов от времени.

В установившемся (статическом) режиме, когда сигналы не изменяются, все производные равны нулю. В нашем случае, приняв 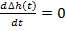в (6.7), получаем

(6.7)

Эта зависимость между установившимися значениями входа Q и выхода h называется статической характеристикой. Она позволяет для любого заданного постоянного значения Q на входе получить значение выхода h.

Теперь предположим, что задана некоторая рабочая точка, то есть, значения входа и выхода удовлетворяют уравнению (6.7), и система все время работает около этого положения равновесия. Вблизи этой точки

где и – малые отклонения входа и выхода от рабочей точки.

Дальше для линеаризации используется разложение функций в ряд Тейлора.

Применив ряд Тейлора при малих значениях получем

(6.8)

Приминим формулу (8) для линеаризации правой части уравнения (6.6), где в роли x выступает расход Q, а в роли y – уровень h. Выполняя дифференцирование, находим

Тогда с помощью формулы (6.8) получаем

.

Подставим 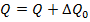и в уравнение (6.6) и учтем, что .

Тогда

.

Вспоминая, что Q₀и h₀ соответствуют статическому режиму, то есть , получаем линеаризованное уравнение в отклонениях от рабочей точки:

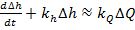(6.9)

где Заметим, что коэффициент k_h зависит от h₀, то есть от выбора рабочей точки. В этом проявляется нелинейность объекта. .

Таким образом, окончательно получаем линеаризованную модель

(6.10)

Но нужно помнить, что это уравнение в отклонениях, и оно справедливо только при малых отклонениях от рабочей точки (Q_0,h₀). При выборе другой рабочей точки коэффициент k_h получится другой.

Дата добавления: 2014-12-23