Оценка состояния САУ

Требования к управлению

Анализ систем управления

Что мы хотим от управления? Это зависит, прежде всего, от решаемой задачи. В задаче стабилизации наиболее важны свойства установившегося режима. Для следящих систем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки).

В целом можно выделить четыре основных требования:

• точность – в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую;

• устойчивость – система должна оставаться устойчивой на всех режимах, не должна идти «вразнос» (корабль не должен идти по кругу при смене курса);

• качество переходных процессов – при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;

• робастность – система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировании.

В системах автоматического управления качественное управление невозможно без точной и своевременной оценки состояния объекта управления и системы в целом. Без датчиков не обходится ни одна САУ с обратной связью. Качественные измерения – основа любой системы управления. Невозможно обеспечить точность управления выше точности измерения. Точность измерения регулируемой величины это верхняя граница точности регулирования, обычно недостижимой в реальных САУ.

Оценка погрешностей измеряемых величин является, таким образом, неотъемлемой частью практически каждой САУ. Поэтому в задачу анализа и синтеза САУ входит не только знакомство с методами и средствами измерений, но и обучение методам определения ошибок, возникающих в процессе проведения измерений различными измерительными приборами.

Настоящая лабораторная работа содержит в себе основные принципы оценки погрешностей в ходе обработки результатов измерений, выполняемых при разработке и функционировании САУ.

Любое измерение производится с какой-то степенью точности. Это связано с несовершенством измерительных приборов, методики измерений, несовершенством органов человеческих чувств и т.п. При этом измеренная величина всегда отличается от ее истинного значения. Другими словами, всякое измерение характеризуется наличием ошибок - погрешностей. Во многих случаях погрешности оказываются весьма значительными. Поэтому в задачу инженера-проектировщика помимо измерения искомой величины в обязательном порядке входит оценка погрешности полученного результата. Без такой оценки невозможно определить качество будущей САУ, а сама система управления не имеет, как правило, практической ценности.

Обычно значение измеренной величины X записывают в следующем виде:

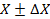где Δ Х - абсолютная погрешность измерения, характеризующая отклонение измеренного значения данной величины от ее истинного значения. При этом, поскольку истинное значение остается неизвестным (т.к. в принципе нельзя осуществить абсолютно точное измерение), можно дать лить приближенную оценку абсолютной погрешности.

Поскольку причины возникновения ошибок могут быть самыми разными, необходимо классифицировать погрешности, возникающие в ходе измерений. Только в этом случае возможна правильная оценка погрешности полученного результата, так как от типа погрешностей зависит и способ их вычисления.

Погрешности подразделяются на случайные и систематические.

Систематической погрешностью называют составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины. Случайной погрешностью называют составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины. Выделяют также погрешности приборов, которые могут иметь как систематический, так и случайный характер.

Рассмотрим некоторые причины, вызывающие появление систематических и случайных погрешностей. Систематическая погрешность может быть связана с неисправностями измерительных приборов, неточностью их регулировки, несоблюдением условий их эксплуатации и т.п. Заметим, что указанные погрешности не относятся к разряду приборных, которые характеризуют вполне исправные и правильно эксплуатируемые инструменты.

Причина возникновения систематической погрешности может заключаться и в самой методике измерений. Так, например, определяя плотность твердого тела по измерениям его массы и объема, можно допустить ошибку, если внутри исследуемого тела имеются пустоты в виде пузырьков воздуха. В этом случае устранить ошибку можно только изменив метод измерений.

Случайные погрешности связаны с некоторыми случайными факторами, влияющими на точность измерений. Они могут зависеть от условий, в которых производятся измерения. Например, обычный сквозняк в производственном помещении может случайным образом сказаться на измерениях температуры. Внешние шумы и электрические наводки так же служат источником случайных погрешностей.

Основным способом уменьшения случайных погрешностей является многократное измерение одной и той же физической величины. Заметим, однако, что максимально возможная точность измерения определяется теми датчиками, которые используются в САУ. Поэтому уменьшение случайной погрешности путем увеличения числа измерений имеет смысл до тех пор, пока ее величина не станет явно меньше величины погрешности датчика. Погрешности датчиков связаны с несовершенством любого измерительного инструмента.

Для повышения точности измерений (если, конечно, этом есть необходимость) следует по возможности устранить погрешности. Это можно сделать различными способами. Если известна природа такой ошибки, и может быть определена ее величина, достаточно ввести соответствующую поправку. Это возможно, например, для исключения влияния на результат измерения таких факторов, как температура и давление воздуха, или факторов, связанных с известным недостатком измерительного инструмента. Разумеется, что вносить такого рода поправки есть смысл только в том случае, когда их величина соизмерима с величиной других ошибок, сопровождающих данные измерения.

Можно также исключить некоторые виды систематических погрешностей, используя специальные методы измерений. Есть и другие способы исключения систематических погрешностей. Однако, как было отмечено выше, всегда остается ошибка; связанная с погрешностью используемого прибора, а также случайные погрешности, которые заранее учесть нельзя.

В том случае, если погрешность прибора заведомо больше величины случайных погрешностей, присущих данному методу при данных условиях измерений, достаточно выполнить измерение один раз. Тогда абсолютная погрешность измерения будет равна погрешности датчика. Если, наоборот, определяющей является случайная погрешность, надо уменьшить ее величину с помощью многократных измерений. Рассмотрим методику оценки случайной погрешности в этом случае.

Предположим, что мы произвели n прямых измерений величины Х. Обозначим через Х₁, Х₂,... Х_n результаты отдельных измерений, которые вследствие наличия случайных погрешностей будут в общем случае неодинаковыми. В теории вероятностей доказывается, что истинное значение измеряемой величины (при отсутствии систематических погрешностей) равно ее среднему значению, получаемому при бесконечно большом числе измерений, т.е.

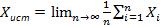(5.1)

Поэтому наиболее близким Х истинному будет для данной серии измерений среднее арифметическое значение, а именно:

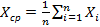(5.2)

Отклонения измеренных значении Х_n от X_ср носят случайный характер и называются абсолютными ошибками отдельных измерений:

(5.3)

В элементарной теории ошибок, мерой случайной погрешности отдельного измерения является так называемая средняя квадратичная погрешность, вычисляем по формуле

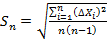(5.4)

При большом числе измерений величина S_n стремится к некоторому пределу σ, т.е.

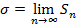
Строго говоря, именно этот предел называется средней квадратичной погрешностью, а квадрат этой величины - дисперсией измерений.

Однако средняя квадратичная погрешность отдельного измерения S _n полезна лишь для оценки точности применяемого способа измерений. Нас же, главным образом, интересует погрешность результата всей серии измерений. Для этого надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение Х_ср от истинного значения искомой величины. Из закона сложения ошибок вытекает, что средняя квадратичная погрешность среднего арифметического равна

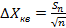(5. 5)

Отсюда следует, что чем больше проделано измерений одной и той же величины, тем меньше случайная погрешность результата. Это вполне понятно, т.к. согласно (5.1) и (5.2), чем больше число опытов, тем ближе Х _ср к Х _ист. Это фундаментальный закон возрастания точности при росте числа наблюдений.

Используя соотношения (5.4) и (5.5), можно записать следующее окончательное выражение для средней квадратичной погрешности результата серии измерений

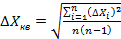(5.6)

Это не означает, однако, что истинное значение измеряемой величины обязательно будет заключено в интервале от X _ср - Δ X _кв до Х _ср + Δ X _кв. Оказывается, что даже при очень большом числе измерений вероятность того, что истинное значение попадет в указанный интервал, не превышает 0,7. Другими словами, надежность полученного результата в данном случае составляет около 70 %. При малом числе измерений (n < 10) она будет еще меньше.

Вероятность того, что истинное значение измеряемой величины попадет в заданный интервал, называется доверительной вероятностью, или коэффициентом доверия α, а соответствующий интервал, определяемый величиной абсолютной погрешности – доверительным интервалом. Достоверность результата при данном количестве измерений можно увеличить, уменьшая его точность, т.е. расширяя доверительный интервал.

Обычно случайную погрешность рассчитывают по формуле:

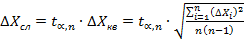(5.7)

где t_α,n — коэффициент Стьюдента, зависящий от числа измерений n и выбранного значения доверительной вероятности α. Значения α и n для ряда случаев приведены в таблице I.

Величина α означает вероятность того, что результат измерений отличается от истинного на величину, не большую, чем Δ X _кв.

Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью X _ист попадает в этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительно величины X _ист.

Чтобы окончательно установить границы доверительного интервала необходимо расширить его с учетом систематической погрешности 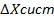. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы. Обычно суммарная погрешность определяется как корень квадратный из суммы квадратов случайной и систематической погрешностей:

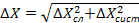(5.8)

Таблица 5.I. Коэффициенты Стьюдента

a =0,68	a =0,95	a =0,99
n	ta,n	n	ta,n	n	ta,n
	2,0		12,7		63,7
	1,3		4,3		9,9
	1,3		3,2		5,8
	1,2		2,8		4,6
	1,2		2,6		4,0
	1,1		2,4		3,7
	1,1		2,4		3,5
	1,1		2,3		3,4
	1,1		2,3		3,3
	1,1		2,1		3,0
	1,1		2,1		2,9
	1,1		2,0		2,8
	1,0		2,0		2,6

Как видно из таблицы, увеличение числа опытов позволяет при заданной доверительной вероятности существенно уменьшить случайную погрешность.

Таким образом, для характеристики величины случайной погрешности в принципе необходимо задать два числа: саму погрешность X _кв и доверительную вероятность α, позволяющую оценить степень надежности полученного результата. Необходимая степень надежности определяется спецификой производимых измерений.

Дата добавления: 2014-12-23