
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналитические методы
|
|
|
|
Представим себе бак с жидкостью (рис.11). В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через S, а площадь сечения отверстия – через S0. Построим модель, которая связывает уровень воды в баке h (в метрах) и расход вытекающей воды q (в м3/с). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид
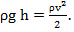 (6.1)
(6.1)
Здесь ρ – плотность жидкости (в кг/м3), g ≈ 9,81 м/с2 – ускорение свободного падения, v – скрость вытекания жидкости (в м/с). Отсюда получаем 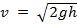 . Учитывая, что расход воды вычисляется как
. Учитывая, что расход воды вычисляется как 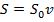 , находим
, находим
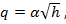 (6.2)
(6.2)
где 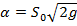 – постоянная величина. Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный
– постоянная величина. Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный
уровень воды и поток вытекающей воды тоже постоянный.
Рис.11 Объект управления- бак с жидкостью
Очевидно, что уравнение (6.2) – нелинейная, поскольку содержит 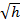 . Линеаризовать ее значит приближенно заменить уравнение (6.2) линейным уравнением q = k
. Линеаризовать ее значит приближенно заменить уравнение (6.2) линейным уравнением q = k  h, где k – некоторый коэффициент. Как его выбрать? На этот вопрос нет однозначного ответа.
h, где k – некоторый коэффициент. Как его выбрать? На этот вопрос нет однозначного ответа.
Предположим, что уровень воды изменяется в интервале от 0 до 1 м. Тогда один из вариантов вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой 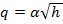 на концах этого интервала. Для определенности далее везде принимаем
на концах этого интервала. Для определенности далее везде принимаем 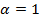 , тогда получаем k =1.
, тогда получаем k =1.
Конечно, эта модель очень грубая и дает большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить k (например, увеличив его до 1, 2), однако точность приближения по-прежнему будет невысока, хотя и чуть-чуть лучше, чем в первом случае.
Рис.12 Кривые q(h) зависимости
Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения h = 0,5 м. В этом случае можно применить другой подход. Заметим, что в этой области кривая 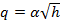 почти совпадает с касательной в точке
почти совпадает с касательной в точке  , угол наклона которой равен производной:
, угол наклона которой равен производной:

Касательная – это прямая с наклоном k, проходящая через точку  , ее уравнение имеет вид q = kh + b. Свободный член b определим из равенства
, ее уравнение имеет вид q = kh + b. Свободный член b определим из равенства
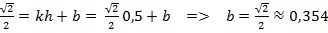 ,
,
так что получаем модель:
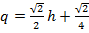 . (6.3)
. (6.3)
Это линейное уравнение, однако модель (6.3) – нелинейная, поскольку для нее не выполняется, например, свойство умножения на константу. Это легко проверить, сравнив U[2h] и 2U[h].
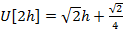 ,
, 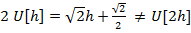 .
.
Принцип суперпозиции также не выполняется.
Для того, чтобы получить из (6.3) линейную модель, нужно записать уравнения в отклонениях от рабочей точки (h0; q0), в которой мы определяли наклон касательной. Из (6.3) следует, что
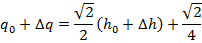
Поскольку график зависимости (6.3) проходит через точку (h0; q0), можно применить равенство
 . (6.4)
. (6.4)
Тогда из (6.4) находим
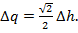 (6.5)
(6.5)
Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки (h0;q0). Приближенная модель (6.5) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от нее ошибка может значительно возрастать.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 520; Нарушение авторских прав?; Мы поможем в написании вашей работы!