Аналитические показатели изменения уровней ряда динамики

Классификация рядов динамики

Ряды динамики. Аналитические показатели ряда динамики. Пример расчётов.

Ряды динамики - это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке.

Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности [6].

Любой ряд динамики состоит из двух элементов:

1. показатель времени ti - это моменты или периоды времени, к которым относятся числовые значения показателей;

2. уровень ряда yi, под которым понимается значение статистического показателя, относящееся к определенному моменту или периоду времени.

Каждый ряд динамики может быть представлен в табличной форме - в виде пар значений ti и yi; и в графической форме - в виде линейной диаграммы.

В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамик абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин – как производные.

Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.

Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей

интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.

Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.

В зависимости от того, как выражаются уровни ряда на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину на определенные интервалы времени (например за сутки, месяц, год и. т. п.), различают соответственно моментные и интервальные ряды динамики.

В моментных рядах уровни выражают состояние явления на критический момент времени – начало месяца, квартала, года и т.д.

Например, численность населения, численность работающих и т.д. В таких рядах каждый последующий уровень полностью или частично содержит значение предыдущего уровня, поэтому суммировать уровни нельзя, так как это приводит к повторному счету. Особенность моментного ряда состоит в том, что его уровни, как правило, содержат элементы повторного счета, например число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности в июне. В результате чего суммировать уровни ряда не целесообразно.

Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным. Это ряды показателей объема производства, объема продаж по месяцам года, количества отработанных человеко-дней и т.д. Особенность интервального ряда состоит в том, что его уровни характеризуют собой суммарный итог какого либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, их можно суммировать, как не содержащие повторного счета.

На практике для количественной оценки динамики явлений широко применяется

ряд основных аналитических показателей.

К таким показателям относятся [4]:

· - абсолютный прирост Δyi;

· - темп роста Ti (коэффициент роста Ki);

· - темп прироста Ti' (коэффициент прироста Ki');

· - абсолютное значение одного процента прироста Ai;

При этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.

Абсолютный прирост (∆y) характеризует размер увеличения (или уменьшения)
уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых
уровней и выражает абсолютную скорость роста. В общем случае абсолютный прирост
может быть представлен в виде:

∆_i = y_i – y_i-k, (2.1.)

где y_i - текущий уровень ряда динамики; i = 2,3,..., n; k = l,2,...,n-l.

При k = 1 от текущего уровня y_i вычитается предыдущий уровень y_i-k, и получается формула для расчета цепного абсолютного прироста:
∆_ц = y_i – y_i-1 (2.2.)

При k = i-1 из формулы (2.1) вытекает выражение для базисного абсолютного при­роста, определяемого относительно начального уровня ряда:

∆_б = y_i – y₁ (2.3.)

Для записи формулы базисного абсолютного прироста в более общем виде уровень y₁ в формуле (2.3) может быть заменен на уровень ряда динамики, принятый за базу срав­нения – у₀:

∆_б = y_i – y₀ (2.4.)

Показатель интенсивности изменения уровня ряда - в зависимости от того, выра­жается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста. Иными словами, коэффициент роста и темп роста представляют собой две формы выражения интенсивности изменения уровня. Разница между ними за­ключается только в единице измерения.

Коэффициент роста показывает, во сколько раз данный уровень ряда больше ба­зисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).

Темпы роста характеризуют отношение двух сравниваемых уровней ряда в виде:

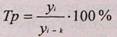(2.5.)

где y_i — текущий уровень ряда динамики; i = 2,3,...,n; k = 1,2,...,п-1.

Отметим, что индекс уровня y_i-k, находящийся в знаменателе, определяется так же, как и в случае абсолютного прироста. Следовательно, из выражения формулы (2.6) в зави­симости от значений индекса к получаются формулы для расчета цепных и базисных тем­пов роста.

Цепной темп роста будет равен:

(2.6.)

Базисный темп роста может быть представлен в виде:

(2.7.)

где y₁ - уровень ряда динамики, принятый за базу сравнения.

Темп роста всегда число положительное. Если темп роста равен 100%, то значение уровня не изменилось, если больше 100%, то значение уровня повысилось, а если меньше 100% - понизилось.

Темп прироста характеризует абсолютный прирост в относительных величинах. Определенный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Темп прироста рассчитывается как отношение абсолютного прироста к уровню, принятому за базу сравнения:

(2.8.)

где y_i — текущий уровень ряда динамики; i = 2,3,...,n; k = 1,2,...,n-1.

Если темп роста всегда положительное число, то темп прироста может быть поло­жительным, отрицательным и равным нулю.

При k = 1 получаем цепной темп прироста:

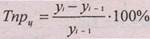(2.9.)

Преобразовав выражение формулы (2.9), можно показать зависимость цепного темпа прироста от соответствующего темпа роста:

(2.10.)

где Тр_ц – цепной темп роста.

Базисный темп прироста равен отношению базисного абсолютного прироста к уровню ряда, принятому за базу сравнения:

(2.11.)

По аналогии с формулой (2.11) получаем:

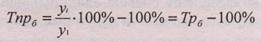(2.12.)

где Тр_б – базисный темп роста.

Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что в реальных экономических процессах замедление темпов прироста не все­гда сопровождается уменьшением абсолютных приростов. Поэтому на практике часто про­водят сопоставление этих показателей. Для этого рассчитывают абсолютное значение од­ного процента прироста. Оно представляет собой одну сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу прироста:

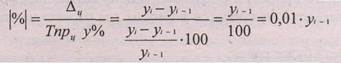(2.13.)

Таким образом, базисные показатели динамики характеризуют окончательный ре­зультат всех изменений в уровнях ряда от периода, к которому относится базисный уро­вень, до данного (i-ro) периода. Цепные показатели динамики характеризуют интенсив­ность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени (рис. 2.1).

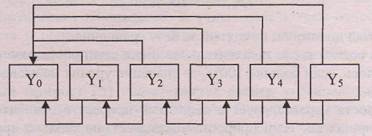
Рис. 2.1. Построение цепных и базисных аналитических показателей динамики

Пример:

Таблица 10

Динамика производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

Год
Объём производства продукции, млн. руб.	10,0	10,7	12,0	10,3	12,9	16,3	15,6	17,8	18,0	18,7

Исходя из данных об объёмах производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг. необходимо:

Определить следующие аналитические показатели ряда динамики цепным и базисным способами: а) абсолютные приросты; б) темпы роста и прироста; в) абсолютное значение 1% прироста;

Решение:

Рассчитаем цепные и базисные абсолютные приросты (формулы 2.2 и 2.3):
Цепные:

∆_{ц 98/97}=10,7-10,0 = 0,7 млн. руб

∆_ц99/98=12,0-10,7=1,3 млн. руб

и т.д.

Базисные:

∆_{б 98/97}= 10,7-10,0 = 0,7 млн. руб

∆_б99/97=12,0-10,0=2 млн. руб

и т.д.

• Рассчитаем цепные и базисные темпы роста (формулы 2.6 и 2.7):

Цепные:

ТР _{ц 98/97}=10,7/10,0*100%=107%

ТР _{ц 99/98}=12/10,7*100%=112,1%

и т.д.

Базисные:

ТР _{б 98/97}=10,7/10,0*100%=107%

ТР _{б 99/97}=12/10,0*100%=120%

и т.д.

• Рассчитаем цепные и базисные темпы прироста (формулы 2.10 и 2.12):
Цепные:

ТПр _{ц 98/97}= 107%-100%=7%

ТПр _{ц 99/98}= 112,1%-100%=12,1%

и т.д.

Базисные:

ТПр _{б 98/97}= 107%-100%=7%

ТПр _{б 99/98}= 120%-100%=20%

и т.д.

• Рассчитаем абсолютное значение одного процента прироста (формула 2.13):

|%|₉₈=10*0,01=0,1

|%|₉₉=10,7*0,01=0,107

Сведем все показатели в таблицу 11.

Таблица 11

Год	Объем производства продукции, млн. руб.	Абсолютный прирост, млн. руб	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста, млн. руб
		Цепной	Базисный, по сравнению с 1997г.	Цепной	Базисный, по сравнению с 1997г.	Цепной	Базисный, по сравнению с 1997г.
		-	-			-	-	-
	10,7	0,7	0,7					0,1
		1,3		112,1		12,1		0,107
	10,3	-1,7	0,3	85,8		-14,2		0,12
	12,9	2,6	2,9	125,2		25,2		0,103
	16,3	3,4	6,3	126,4	126,3	26,4	26,3	0,129
	15,6	-0,7	5,6	95,7		-4,3		0,163
	17,8	2,2	7,8	114,1		14,1		0,156
		0,2		101,1		1,1		0,178
	18,7	0,7	8,7	103,9		3,9		0,18

Рассмотрим графики, изображённые на рисунках 2-6. Они отображают изменение аналитических показателей данного ряда динамики.

Рис.2 График объема производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

Рис.3 График абсолютного прироста производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

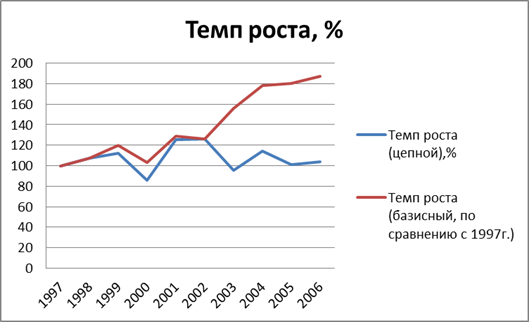
Рис.4 График темпа роста производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

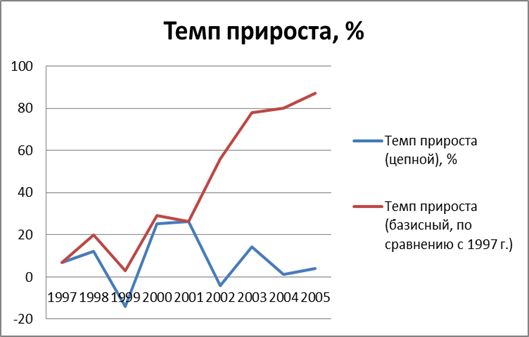
Рис.5 График темпа прироста производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

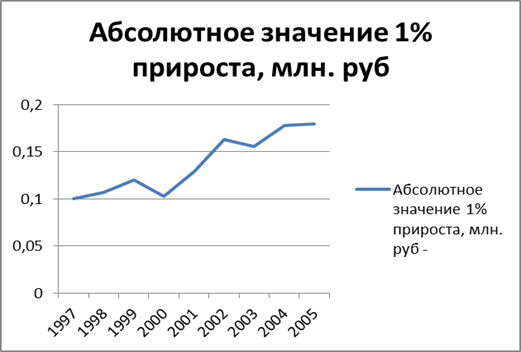
Рис.6 График абсолютного значения 1% прироста производства рыбной продукции предприятием ЗАО «АРХРЫБПРОМ» Архангельской области за 1997-2006 гг.

Дата добавления: 2014-12-23