Результаты ранжирования выборочных данных и вычисление моды и медианы

Используя исходные данные, запишем все заданные значения выборки в виде неубывающей последовательности значений случайной величины X, представленные в табл. 5.

Интервал [ 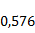; ], содержащий все элементы выборки, разобьём на частичные интервалы, используя при этом формулу Стерджеса для определения оптимальной длины и границ этих частичных интервалов.

По формуле Стерджеса длина частичного интервала равна:

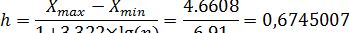
Для удобства и простоты расчётов округлим величину .В нашем случае выбираем h=0,7и вычисляем границы интервалов.

Таблица 5

Ранжированный ряд

	0,576		2,6859		3,3666
	1,1372		2,7072		3,5415
	1,4869		2,721		3,5548
	1,556		2,7762		3,6123
	1,594		2,7794		3,6264
	1,6765		2,7971		3,6794
	1,8736		2,8279		3,7532
	2,185		2,8539		3,7662
	2,1924		2,9234		3,8633
	2,2663		2,9355		3,9122
	2,3384		3,0442		3,9321
	2,3479		3,0581		3,9967
	2,4139		3,065		4,0016
	2,4573		3,0828		4,2159
	2,5291		3,0918		4,2594
	2,5387		3,1033		4,5374
	2,5458		3,1401		4,622
	2,5754		3,2267		4,7382
	2,6255		3,2481		4,7513
	2,664		3,3269		5,2368

За начало первого интервала принимаем значение

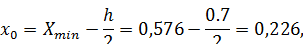
которое округляем до целого значения и принимаем . Далее вычисляем границы интервалов:

;

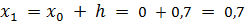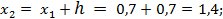
Вычисление границ заканчиваем, как только выполняется неравенство

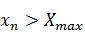, то есть

После определения частичных интервалов, определяем экспериментальные частоты , равные числу членов вариационного ряда, попадающих в этот интервал:

где , - границы i -го интервала; - значения вариационного ряда.

Набор частот 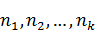должен удовлетворять равенству:

…

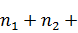Относительной частотой 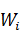называют долю наблюдений, попадающих в рассматриваемый интервал:

Плотность распределения относительных частот определим как отношение относительных частот к величине интервала:

,

где является серединой интервала

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны эмпирической плотности распределения:

,

где i =1,2,…, k.

Площадь i-го прямоугольника равна доле случайных величин, попавших в i-йинтервал:

.

Площадь гистограммы относительных частот равна сумме площадей прямоугольников:

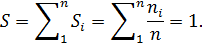
Таким образом, функция 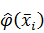является статистическим аналогомплотности распределения случайной величины Х,реализации которой получают при статистическом наблюдении.

Полигоном частот называется ломаная линия, отрезки которой соединяют середины горизонтальных отрезков, образующих прямоугольники в гистограмме.

Полигоном относительных частот называется ломаная линия свершинами в точках: ; .

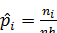По результатам вычислений составим табл. 6 значений выборочной функции плотности.

Таблица 6

Значения выборочной функции плотности

	[0; 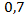)	[ ;1,4)	[1,4;2,1)	[2,1;2,8)	[2,8;3,5)	[3,5;4,2)	[4,2;4,9)	[4,9;5,6)
	0,5	1,05	1,75	2,45	3,15	3,85	4,55	5,25
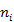
	0,01666	0,01666	0,08333	0,31666	0,25	0,2	0,1	0,01666
	0,0238	0,0238	0,11904	0,45237	0,35714	0,28571	0,14286	0,0238

В первую строку таблицы поместим частичные интервалы, во вторую строку - середины интервалов, в третью строку запишем частоты -количество элементов выборки, попавших в каждый частичный интервал, в четвёртую строку запишем относительные частоты, в пятую строку запишем значения плотности относительных частот или значения выборочной, экспериментальной функции плотности.

По результатам вычислений функции плотности, представленным в табл. 6, можно сделать вывод, что мода имеет один локальный максимум в окрестностях точки х = 2,45 с частотой 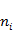= 19.

Оценку медианы находим, используя вариационный ряд, для которого n= 2k = 60 и k= 30:

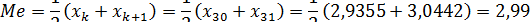
Сравнение оценок медианы Ме= 2,99 и оценки математического ожидания 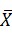= 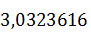показывает, что они отличаются на 1,4 %.

Дата добавления: 2014-12-23