
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Параметрическая оценка функции плотности распределения
|
|
|
|
Предположим, что статистические наблюдения принадлежат к нормальному закону распределения с функцией плотности в виде:
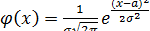 ,
,
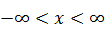 ,
,
где а=М(Х) - математическое ожидание случайной величины Х; 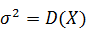 -дисперсия случайной величины Х.
-дисперсия случайной величины Х.
Значения математического ожидания а и дисперсии 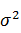 являются основными числовыми характеристиками случайной величины.
являются основными числовыми характеристиками случайной величины.
До проведения статистического наблюдения конкретные значения математического ожидания а и дисперсии 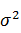 неизвестны.
неизвестны.
Поэтому особенно важно знать эти числовые характеристики до начала статистической обработки выборочных наблюдений. В качестве оценок параметров а и 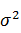 будем использовать
будем использовать 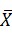 и
и 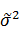 .
.
Исходя из гипотезы, что заданная выборка имеет нормальный закон распределения, найдём параметрическую оценку функции плотности, используя формулу для плотности распределения вероятности нормального закона:
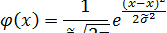
где 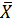 =
= 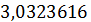 и
и 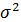 =
= 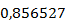 .
.
Значения этой функции вычисляют для середин частичных интервалов, т.е. при 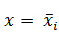 . На практике для упрощения вычислений
. На практике для упрощения вычислений
функции 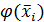 , где i= 1,2,..., k, пользуются таблицами значений функции плотности стандартной нормальной величины (табл.7).
, где i= 1,2,..., k, пользуются таблицами значений функции плотности стандартной нормальной величины (табл.7).
Для этого вычислим значения
 дляi= 1,2,..., k:
дляi= 1,2,..., k:
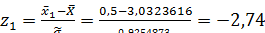 ;
;
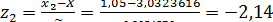 ;
;
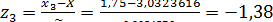 ;
;
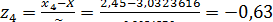 ;
;
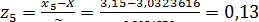 ;
;
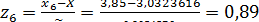 ;
;
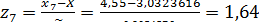 ;
;
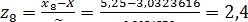 .
.
Таблица 7
Плотность вероятности нормального распределения 
| г | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0.1 | ||||||||||
| 0,2 | 3894| | |||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ОНО | |||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0014 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Затем по табл.7 находим значения функции плотности стандартной нормальной величины
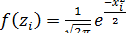 .
.
Имеем:
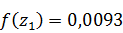 ;
;
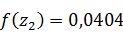 ;
;
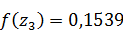 ;
;
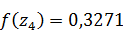 ;
;
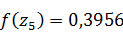 ;
;
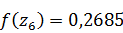 ;
;
 ;
;
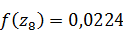 ;
;
После этого, разделив значения функции 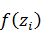 на
на 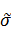 , получим значения теоретической функции плотности
, получим значения теоретической функции плотности 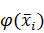 :
:
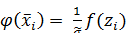 .
.
Имеем:
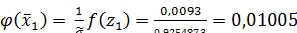 ;
;
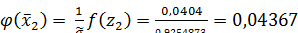 ;
;
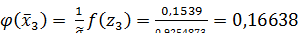 ;
;
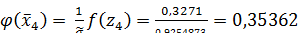 ;
;
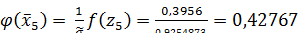 ;
;
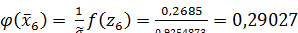 ;
;
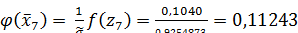 ;
;
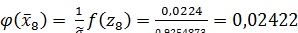 .
.
Функция 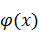 принимает наибольшее значение при
принимает наибольшее значение при 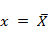 :
:
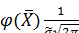 .
.
Если h мало и объём выборки n велик, то можно приближенно, достаточно близко определить вероятность того, что случайная величина Х принадлежит интервалу 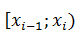 , по формуле:
, по формуле:
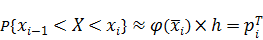 ,
,
где 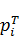 - теоретическая вероятность.
- теоретическая вероятность.
Используем соотношение, связывающее теоретическую вероятность 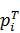 с теоретической частотой
с теоретической частотой 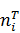 :
:
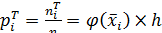 .
.
Тогда теоретические частоты 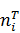 определяются равенствами
определяются равенствами
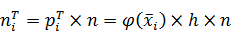 .
.
Может оказаться, что теоретические частоты 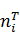 являются дробными
являются дробными
числами, но число элементов выборки, попадающих в i-й интервал, всегда является целым числом. Поэтому округлим дробные теоретические частоты 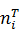 до целых значений с условием, чтобы сумма всех найденных теоретических частот была близка к п:
до целых значений с условием, чтобы сумма всех найденных теоретических частот была близка к п:
 .
.
Если сумма теоретических вероятностей существенно ниже единицы, то надо построить дополнительные интервалы слева и справа от основного интервала [ 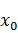 ;
; 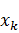 ).Для средних значений частичных интервалов, построенных слева и справа от интервала [
).Для средних значений частичных интервалов, построенных слева и справа от интервала [ 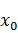 ;
; 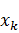 ), вычислим значения теоретической плотности нормального распределения и теоретические частоты. Сумма для всех теоретических вероятностей должна быть близка к единице с точностью до нескольких знаков после запятой:
), вычислим значения теоретической плотности нормального распределения и теоретические частоты. Сумма для всех теоретических вероятностей должна быть близка к единице с точностью до нескольких знаков после запятой:
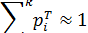
Для того чтобы определить теоретические вероятности, используют таблицу значений функции плотности стандартной нормальной величины:
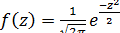 .
.
Вычислим теоретические вероятности:
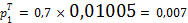 ;
;
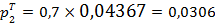 ;
;
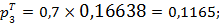
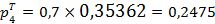 ;
;
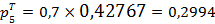 ;
;
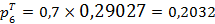
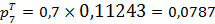 ;
;
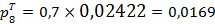 .
.
Вычислим теоретические частоты 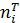 для n=60:
для n=60:
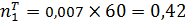 ;
;
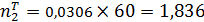 ;
;
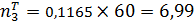 ;
;
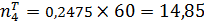 ;
;
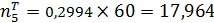 ;
;
 ;
;
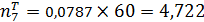 ;
;
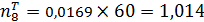 ;
;
Результаты вычислений вероятностей и соответствующих частот приведены в табл. 8
В первом столбце таблицы расположены k частичных интервалов, во втором столбце расположены наблюдаемые частоты 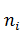 , в третьем столбце расположены координаты середины частичных интервалов, в четвёртом столбце расположены относительные частоты, в пятом столбце расположены значения экспериментальной функции плотности, в шестом столбце расположены значения
, в третьем столбце расположены координаты середины частичных интервалов, в четвёртом столбце расположены относительные частоты, в пятом столбце расположены значения экспериментальной функции плотности, в шестом столбце расположены значения 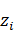 , в седьмом столбце расположены значения теоретической функции плотности, вычисленные в середине частичных интервалов, в восьмом столбце расположены значения теоретических вероятностей, в девятом столбце расположены значения теоретических частот.
, в седьмом столбце расположены значения теоретической функции плотности, вычисленные в середине частичных интервалов, в восьмом столбце расположены значения теоретических вероятностей, в девятом столбце расположены значения теоретических частот.
Таблица 8
Результаты вычисления экспериментальных и теоретических вероятностей и частот
| [хi-1; хi) | ni | 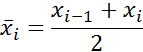
| pi= 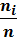
| 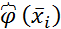
| zi | 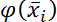
| piT | niT |
[0;  ) )
| 0,5 | 0,01666 | 0,0238 | 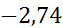
| 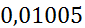
| 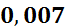
| 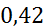
| |
[ 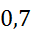 ;1,4) ;1,4)
| 1,05 | 0,01666 | 0,0238 | 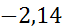
| 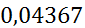
| 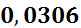
| 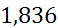
| |
| [1,4;2,1) | 1,75 | 0,08333 | 0,11904 | 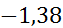
| 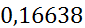
| 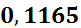
| 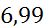
| |
| [2,1;2,8) | 2,45 | 0,31666 | 0,45237 | 
| 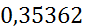
| 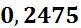
| 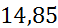
| |
| [2,8;3,5) | 3,15 | 0,25 | 0,35714 | 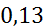
| 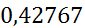
| 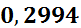
| 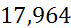
| |
| [3,5;4,2) | 3,85 | 0,2 | 0,28571 | 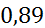
| 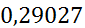
| 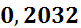
| 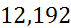
| |
| [4,2;4,9) | 4,55 | 0,1 | 0,14286 | 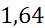
| 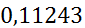
| 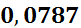
| 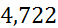
| |
| [4,9;5,6) | 5,25 | 0,01666 | 0,0238 | 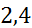
| 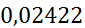
| 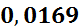
| 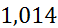
| |
| Σ | 0,9997»1 | 0,9998»1 | 59,988»60 |
Построим графики экспериментальной и теоретической плотности нормального распределения (рис. 1).
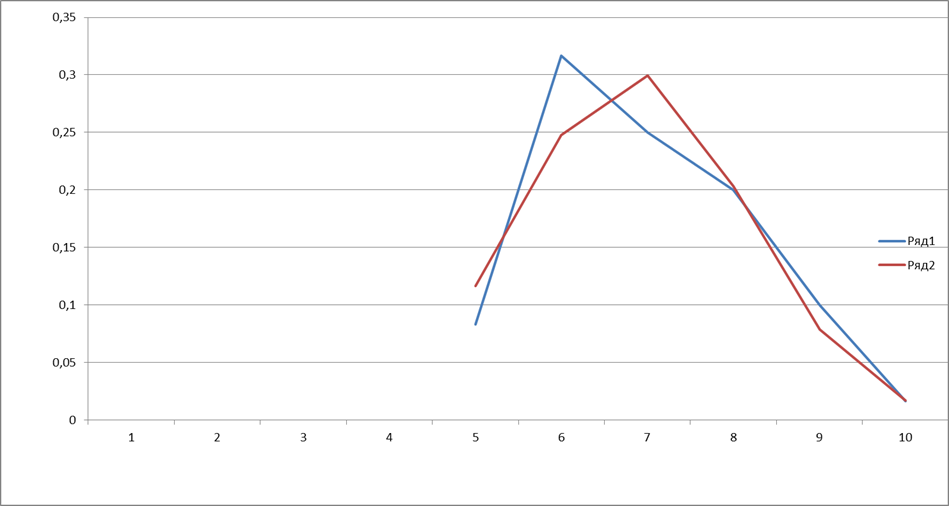
Рис. 1 - Графики экспериментальной и теоретической плотности нормального распределения
Отложим по оси Oх среднее значение i-го частичного интервала  с шагом h; в точках
с шагом h; в точках  по оси ординат отложим вычисленные значенияэкспериментальной и теоретической функций плотности. Соединяя построенные координаты точек на плоскости, получим графики экспериментальной и теоретической функций плотности, которые приведены на рис.1.
по оси ординат отложим вычисленные значенияэкспериментальной и теоретической функций плотности. Соединяя построенные координаты точек на плоскости, получим графики экспериментальной и теоретической функций плотности, которые приведены на рис.1.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1112; Нарушение авторских прав?; Мы поможем в написании вашей работы!