
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Lecture 11
|
|
|
|
.
.14. Коэффициент детерминации представляет собой долю:
а) дисперсии теоретических значений в общей дисперсии
б) межгрупповой дисперсии в общей;
в) межгрупповой дисперсии в остаточной;
г) дисперсии теоретических значений в остаточной дисперсии.
.15. Эмпирическое корреляционное отношение = …. (с точностью до 0,01), если межгрупповая дисперсия составляет 69% от общей дисперсии.
. 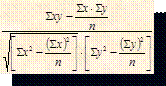 16. Теснота связи двух признаков при нелинейной зависимости определяется по формуле:
16. Теснота связи двух признаков при нелинейной зависимости определяется по формуле:

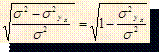 а) б) в)
а) б) в)
17. Прямолинейная связь между факторами исследуется с помощью уравнения регрессии:
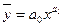
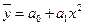 а)
а) 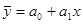 б)
б) 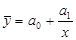 в) г)
в) г)
18. Для измерения тесноты корреляционной связи между двумя количественными признаками используются:
а) коэффициент корреляции знаков;
б) коэффициент эластичности;
в) линейный коэффициент корреляции;
г) коэффициент корреляции рангов.
19.Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения … дисперсии(й):
а) средней из групповых дисперсий к общей;
б) межгрупповой дисперсии к общей;
в) межгрупповой дисперсии к средней из групповых;
г) средней из групповых дисперсий к межгрупповой.
20 Параметр а1(а1 = - 1,04) линейного уравнения регрессии ух = 34,7 – 1.04х показывает, что:
а) с увеличением признака Х на 1 признак У уменьшается на 1,04;
б) с увеличением признака Х на 1 признак У уменьшается на 36,5;
в) связь между признаками Х и У прямая;
г) связь между признаками Х и У обратная.
21. Корреляционный анализ используется для изучения:
а) взаимосвязи явлений;
б) развития явления во времени;
в) структуры явлений.
22. Тесноту связи между двумя альтернативными качественными признаками можно измерить с помощью коэффициентов:
а) знаков Фехнера;
б) корреляции рангов Спирмена;
в) ассоциации;
г) контингенции;
д) конкордации.
23. Парный коэффициент корреляции показывает тесноту:
а) линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
б) линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) связи между результативным признаком и остальными, включенными в модель;
г) нелинейной зависимости между двумя признаками.
24. Применяемый в корреляционном анализе коэффициент Фехнера учитывает только знаки отклонений уровней от средней, но не учитывает величину этих отклонений, поэтому судить по его величине о тесноте связи:
а) вполне можно;
б) можно с вероятностью 0,95;
в) нельзя;
г) можно с коэффициентом доверия t=2.
25. Частный коэффициент корреляции показывает тесноту:
а) линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
б) линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) связи между результативным признаком и остальными, включенными в модель;
г) нелинейной зависимости между двумя признаками.
26. Парный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) любые положительные;
д) любые меньше нуля.
27. Частный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) любые положительные;
д) любые меньше нуля.
28. Множественный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) любые положительные;
д) любые меньше нуля.
29. Коэффициент детерминации может принимать значения:
а) от 0 до 1;
б) от -1 до 0;
в) от -1 до 1;
г) любые положительные;
д) любые меньше нуля.
30. В результате проведения регрессионного анализа получают информацию, описывающую:
а) взаимосвязь показателей;
б) соотношение показателей;
в) структуру показателей;
г) темпы роста показателей;
д) темпы прироста показателей.
31. Рабочему Давыдову при проведении ранжирования рабочих для расчета коэффициента рангов следует присвоить ранг по следующим данным:
| Фамилия | Иванов | Петров | Сидоров | Давыдов | Кузнецов |
| Разряд |
а) 4;
б) 2;
в) 3,5;
г) 3.
32. По аналитическому выражению связи в статистике классифицируются на:
а) сильные и слабые;
б) закономерные и произвольные;
в) прямые и обратные;
г) линейные и криволинейные.
33. Теснота связи между признаками определяется с помощью метода:
а) группировок;
б) средних величин;
в) относительных величин;
г) корреляции.
34. Если результативный и факторный признаки являются количественными, то для анализа тесноты связи между ними могут применяться:
а) корреляционное отношение;
б) линейный коэффициент корреляции;
в) коэффициент ассоциации;
г) коэффициент корреляции рангов Спирмена;
д) коэффициент корреляции рангов Фехнера.
35. Связь между факторным и результативным признаками является тесной, если значение показателя тесноты связи равно:
а) 0,6;
б) 0,75;
в) 0,3;
г) 0,5.
36. Если на результативный признак влияют два фактора, то при проведении КРА строят модели:
а) сложные;
б) парные;
в) однофакторные;
г) многофакторные.
37. Связь является функциональной, если определенному значению факторного признака соответствует:
а) 0 значений результативного признака;
б) несколько значений результативного признака;
в) 2 значения результативного признака;
г) строго определенное значение результативного признака.
38. Если уравнение регрессии между себестоимостью единицы продукции (Y) и производительностью труда одного работника (Х) выглядит следующим образом: Y = 320 – 0,2Х, то при увеличении факторного признака результативный:
а) не изменяется;
б) увеличивается;
в) изменяется произвольно;
г) уменьшается.
Раздел 4. Словарь основных терминов (глоссарий)
Вариация – это изменение величины либо значения признака у отдельных единиц статистической совокупности.
Единицы статистической совокупности – первичные элементы совокупности, являющиеся носителями признаков.
Предмет статистики – количественная сторона массовых социально-экономических явлений и процессов в неразрывной связи с их качественной стороной в конкретных условиях места и времени.
Признак – общие свойства единиц статистической совокупности.
Система статистических показателей – это совокупность взаимосвязанных показателей, отражающая существующие между явлениями взаимосвязи.
Статистическая закономерность – это закономерность, в которой необходимость неразрывно связана в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя как закон.
Статистическая совокупность – масса отдельных единиц, объединенной единой качественной основой, но различающихся между собой по ряду признаков.
Статистический показатель – количественная оценка свойств изучаемого явления.
Единица наблюдения – это первичный элемент объекта статистического наблюдения, являющийся носителем признаков, подлежащих регистрации.
Монографическое наблюдение – это подробное описание отдельных единиц совокупности.
Наблюдение по способу основного массива – при этой форме наблюдения отбирают наиболее крупные единицы наблюдения, которые дают основной вклад в характеристику изучаемого явления.
Несплошное наблюдение – это такое наблюдение, при котором обследованию подвергаются не все единицы совокупности, а только часть их, отобранная в случайном порядке.
Объект статистического наблюдения – совокупность, которая будет подвергнута наблюдению.
Программа наблюдения – перечень показателей, подлежащих регистрации.
Сплошное наблюдение – это такое наблюдение, при котором регистрации подлежат все единицы изучаемой совокупности.
Статистическое наблюдение – процесс собирания данных о массовых явлениях общественной жизни.
Альтернативные признаки – это признаки, которыми одни единицы совокупности обладают, а другие – нет.
Аналитическая группировка – это такая группировка, с помощью которой исследуются взаимосвязи варьирующих признаков в пределах однокачественной совокупности.
Атрибутивные признаки – это признаки, не имеющие количественного значения.
Варианта – это числовое значение количественного признака в вариационном ряду распределения.
Вторичная группировка – образование новых групп на основе ранее проведенной группировки.
Группировка – разделение (или объединение) единиц исследуемой совокупности на группы по существенным для них варьирующим признакам.
Группировочные признаки – это признаки, по которым производится распределение единиц изучаемой совокупности на группы.
Дискретный вариационный ряд – это такой ряд, в котором варианты имеют значение целых чисел.
Интервал группировки – это разница между максимальным и минимальным значениями признака в каждой группе.
Интервальный вариационный ряд – такой ряд, где значения вариант даны в виде интервалов.
Количественные признаки – это признаки, имеющие различные цифровые характеристики у отдельных единиц изучаемой совокупности.
Объем совокупности – сумма всех частот.
Простая группировка – это группировка по одному признаку.
Сложная группировка – это группировка по двум или нескольким признакам.
Статистический ряд распределения – это ряд упорядочено расположенных единиц изучаемой совокупности по какому-либо варьирующему признаку.
Частости – это частоты, выраженные в виде относительных дисциплин (долях единиц или процентах).
Частоты – числа, показывающие, сколько раз повторяются те или иные варианты в ряду распределения.
Абсолютные величины – это первоначальный вид обобщающих показателей, получаемых непосредственно в результате суммирования первичного статистического материала и отражающие физические размеры процессов и явлений.
Обобщающие показатели – это показатели, которыми статистика характеризует совокупности единиц в целом или по группам.
Относительная величина – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых статистических величин.
Относительная величина выполнения плана характеризует отношение уровня, фактически достигнутого в отчетном периоде к запланированному на этот период.
Относительная величина динамики характеризует изменение уровня какого-либо явления во времени и выражается в процентах, коэффициентах.
Относительная величина интенсивности характеризует степень распространения или развития изучаемого явления в определенной среде.
Относительная величина координации характеризует отношение частей изучаемой совокупности к одной из них, принятой за базу сравнения, и показывает, во сколько раз одна часть совокупности больше (меньше) другой.
Относительная величина планового задания характеризует отношение уровня, запланированного на предстоящий период к уровню, фактически сложившемуся в предшествующем периоде.
Относительная величина сравнения характеризует сравнительные размеры двух одноименных абсолютных величин, относящихся к одному периоду времени, но к различным объектам или территориям.
Относительная величина структуры характеризует долю или удельный вес отдельных частей изучаемой совокупности во всем ее объеме.
Статистический показатель – это обобщающая количественная мера какого-то свойства совокупности в конкретных условиях места и времени.
Внутригрупповая дисперсия (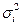 ) - отражает вариацию признака только за счет условий и причин, действующих внутри группы и не зависящую от группировочного признака.
) - отражает вариацию признака только за счет условий и причин, действующих внутри группы и не зависящую от группировочного признака.
Дисперсия признака (s2) - позволяет оценить влияние различных факторов на вариацию признака и определяется на основе квадратической степенной средней. Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности.
Коэффициент вариации (v) - служит характеристикой однородности совокупности, а также позволяет сравнивать колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической.
Медиана (Ме) - это варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам: одна половина единиц совокупности со значениями признака меньше медианного, а у другой половины единиц значение признака не меньше медианного.
Межгрупповая дисперсия (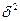 ) характеризует вариацию результативного признака за счет группировочного признака-фактора.
) характеризует вариацию результативного признака за счет группировочного признака-фактора.
Мода (Мо) – это наиболее часто повторяющееся значение признака, это варианта, которой в дискретном ряду распределения соответствует наибольшая частота.
Размах вариации (R) - наиболее простой показатель вариации признака, который исчисляется как разность между наибольшим (xmax) и наименьшим (xmin) значениями варьирующего признака и улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака. Оно показывает, на сколько в среднем отклоняются индивидуальные значения признака от их среднего значения.
Среднее линейное отклонение (d) – показатель вариации, дающий обобщающую характеристику колеблемости всех единиц распределения, рассчитывается по средней арифметической из отклонений (x - 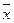 ) индивидуальных значений вариант от средней величины.
) индивидуальных значений вариант от средней величины.
Средняя арифметическая взвешенная - применяется при расчете среднего значения признака по сгруппированным данным, т.е. когда известны варианты и соответствующие им неравновеликие частоты.
Средняя арифметическая простая - наиболее распространенный вид средних степенных, которая применяется в тех случаях, когда известны варианты и соответствующие им частоты, а объем осредняемого признака представляет собой сумму его значений у отдельных единиц изучаемой совокупности.
Средняя величина – это обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку.
Средняя гармоническая - это величина, обратная средней арифметической из обратных значений признака. Она применяется для расчета средней тогда, когда веса приходится не умножать, а делить на варианты.
Средняя геометрическая - применяется чаще всего при расчете среднего значения признака по заданным относительным величинам динамики, исчисленным как отношение каждого уровня ряда динамики к предыдущему.
Средняя квадратическая - используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения.
Бесповторная выборка – когда единицы совокупности, попавшие в выборку, не возвращаются в генеральную совокупность, следовательно, они не могут попасть в новую выборку, а объем генеральной совокупности уменьшается на численность выборочной совокупности.
Выборочная доля (w) - определяется отношением числа единиц, обладающих изучаемым признаком, к общему числу единиц выборочной совокупности.
Выборочная совокупность (n) - часть единиц совокупности, которая подвергается выборочному обследованию.
Выборочная средняя ( ) - среднее значение признака в выборочной совокупности.
) - среднее значение признака в выборочной совокупности.
Выборочное наблюдение – статистическое наблюдение, при котором характеристика всей совокупности единиц дается по некоторой их части, отобранной в случайном порядке.
Генеральная дисперсия (sген.2) - дисперсия признака в генеральной совокупности.
Генеральная доля (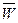 ) - доля единиц, обладающих изучаемым значением признака в генеральной совокупности.
) - доля единиц, обладающих изучаемым значением признака в генеральной совокупности.
Генеральная совокупность (N) – вся изучаемая совокупность единиц.
Генеральная средняя (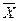 ) – среднее значение признака в генеральной совокупности.
) – среднее значение признака в генеральной совокупности.
Коэффициент кратности ошибки (t) или коэффициент доверия - зависит от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t-кратную среднюю ошибку.
Механическая выборка состоит в том, что вся генеральная совокупность единиц разбивается на равные группы (интервалы) и из каждого интервала (группы) выбирается по одной единице. При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.
Ошибка выборки - расхождение между характеристиками выборочной и генеральной совокупности. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации – ошибки выборки, которые появляются, как правило, из-за неправильных или неточных сведений, невнимательности, некомпетентности регистратора, пропуска или повторного счета некоторых единиц совокупности, описки при заполнении статистических формуляров, несовершенства измерительных приборов и т.п.
Ошибки репрезентативности – это расхождение между значениями показателей выборочной и генеральной совокупностей.
Повторная выборка - когда единицы выборочной совокупности после их регистрации возвращаются в генеральную совокупность и имеют равную возможность наряду с остальными единицами при повторном отборе вновь попасть в выборку, при этом генеральная совокупность единиц остается неизменной.
Предельная ошибка выборки (D) – величина, показывающая предельные отклонения выборочных характеристик от генеральных с определенной степенью вероятности.
Систематические ошибки регистрации – ошибки выборки, которые возникают в результате того, что получаемая информация сознательно тенденциозно искажается.
Систематические ошибки репрезентативности - возникают в связи с нарушением принципа случайности отбора единиц в выборочную совокупность и не поддаются количественной оценке.
Случайные ошибки регистрации – которые могут быть допущены как в большую так и в меньшую стороны в ответах опрашиваемых или регистраторами при заполнении формуляров.
Случайные ошибки репрезентативности - характеризуют размеры отклонения генеральных характеристик от выборочных и означают, что, несмотря на соблюдение принципа случайности отбора единиц, расхождения между характеристиками генеральной и выборочной совокупности будут иметь место из-за того, что совокупность отобранных единиц наблюдения не полностью воспроизводит генеральную.
Собственно-случайный отбор - выборочная совокупность образуется в результате случайного отбора отдельный единиц из генеральной совокупности без предварительного расчленения ее на какие-либо группы, и единица отбора совпадает с единицей наблюдения.
Средняя ошибка выборки (μ) – количественное измерение возможных расхождений между характеристиками выборочной и генеральной совокупности.
Базисные индексы – индексы с постоянной базой сравнения, показывающие изменение уровня показателя во всех последующих периодах по сравнению с начальным, принятым за базу.
Индекс – это относительный показатель сравнения двух совокупностей, характеризующий изменение величины простого явления, состоящего из элементов, которые можно суммировать, или сложного явления, элементы которого непосредственно не суммируются.
Индивидуальные индексы дают сравнительную характеристику изменения во времени (или в пространстве) отдельных элементов той или иной совокупности
Общие индексы характеризуют изменение сложной совокупности в целом, отдельные элементы которой непосредственно несоизмеримы
Цепные индексы – индексы с переменной базой сравнения, показывающие изменение уровня показателя год за годом (месяцем, кварталом).
Абсолютный прирост - показатель динамики, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Базисный показатель - показатель, вычисляемый при сравнении каждого уровня ряда с одним и тем же базисным уровнем; используется для расчета показателей динамики на постоянной базе.
Интервальный ряд динамики - ряд динамики, отражающий итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Коэффициент роста - темп роста, выраженный в виде коэффициента.
Моментный динамический ряд - ряд динамики, отражающий состояние изучаемых явлений на отдельные даты (моменты) времени.
Равнозамедленное развитие - тип динамики, которому свойственно постоянное во времени замедление развития.
Равномерное развитие - тип динамики, которому присущ постоянный абсолютный прирост.
Равноускоренное развитие - тип динамики, которому свойственно постоянное во времени увеличение развития.
Развитие по экспоненте - тип динамики, характеризующийся стабильными темпами роста.
Ряд динамики (временной ряд) - это ряд расположенных в хронологической последовательности статистических показателей.
Способ скользящей средней - метод состоящий в том, что вместо каждого уровня исходного ряда берутся средние из уровней рядом стоящих периодов, причем период осреднения все время меняется: из него вычитается один член и прибавляется следующий.
Способ укрупнения интервалов - метод, состоящий в том, что первоначальный ряд динамики преобразуется в ряды более продолжительных периодов.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
Средний темп роста - обобщенная характеристика индивидуальных темпов роста ряда динамики.
Средний уровень ряда динамики характеризует типичную величину абсолютных уровней.
Темп роста - статистический показатель динамики, характеризующий отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Тренд - общая тенденция развития.
Уровни ряда динамики отражают количественную оценку (меру) развития во времени изучаемого явления.
Цепной показатель - показатель, вычисляемый при сравнении каждого последующего уровня ряда с предыдущим; используется для расчета показателей динамики на переменной базе.
Корреляционная связь - это связь, при которой определенному значению факторного признака соответствует лишь среднее значение результативного признака
Корреляционно-регрессивный анализ включает в себя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Множественной корреляцией называется зависимость результативного и двух или более факторных признаков, включенных в исследование.
Парной корреляцией называется связь между двумя признаками (результативным и факторным или двумя факторными)
Регрессивный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов применяется за постоянные (или усредненные) величины
Результативными (Y)называются признаки, изменяющиеся под действием других, связанных с ними признаков
Теснота связи количественно выражается величиной коэффициентов корреляции.
Факторными (Х) называются признаки, обуславливающие изменение результативных признаков
Функциональная связь - это связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
РАЗДЕЛ 5. Методические указания для выполнения контрольных, курсовых и выпускных квалификационных работ
По дисциплине «Статистика» в соответствии с учебным планом контрольная работа отсутствует. Курсовые и выпускные квалификационные работы также отсутствуют.
Раздел 6. Данные о мультимедийных лекциях
Диск с мультимедийными лекциями прилагается (на кафедре)
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1103; Нарушение авторских прав?; Мы поможем в написании вашей работы!