
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Connectedness in undirected graphs
|
|
|
|
Paths
A path of length n from u to v, where n is a positive integer, in an undirected graph is a sequence of edges  of the graph such that
of the graph such that  where
where 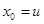 and
and 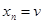 . When the graph is simple, we denote this path by its vertex sequence
. When the graph is simple, we denote this path by its vertex sequence 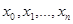 (since listing these vertices uniquely determines the path). The path is a circuit if it begins and ends at the same vertex, that is, if u = v. The path or circuit is said to pass through or traverse the vertices
(since listing these vertices uniquely determines the path). The path is a circuit if it begins and ends at the same vertex, that is, if u = v. The path or circuit is said to pass through or traverse the vertices 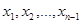 . A path or circuit is simple if it does not contain the same edge more than once.
. A path or circuit is simple if it does not contain the same edge more than once.
Example.
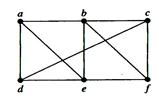
In this simple graph a, d, c, f, e is a simple path of length 4, since { a, d }, { d, c }, { c, f } and { f, e } are all edges. However, d, e, c, a is not a path, since { e, c } is not an edge. Note that b, c, f, e, b is a circuit of length 4 since { b, c }, { c, f }, { f, e } and { e, b } are edges, and this path begins and ends at b. The path a, b, e, d, a, b, which is of length 5, is not simple since it contains the edge { a, b } twice.
A path from a to b in a directed graph G is a sequence of one or more edges 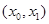 ,
, 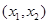 ,
, 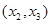 , …,
, …, 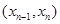 in G, where
in G, where  and
and 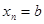 , that is, a sequence of edges where the terminal vertex of an edge is the same as the initial vertex in the next edge in the path. This path is denoted by
, that is, a sequence of edges where the terminal vertex of an edge is the same as the initial vertex in the next edge in the path. This path is denoted by  and has length n. A path that begins and ends at the same vertex is called a circuit or cycle.
and has length n. A path that begins and ends at the same vertex is called a circuit or cycle.
A path of length n from u to v in a directed multigraph is a sequence of edges  of the graph such that
of the graph such that 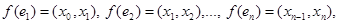 where
where 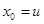 and
and 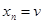 . When there are no multiple edges in the graph, this path is denoted by its vertex sequence
. When there are no multiple edges in the graph, this path is denoted by its vertex sequence 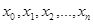 . A path or circuit is called simple if it does not contain the same edge more than once.
. A path or circuit is called simple if it does not contain the same edge more than once.
An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph.
Example.
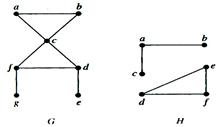
The graph G is connected, since for every pair of distinct vertices there is a path between them. However, the graph H is not connected. For instance, there is no path in H between vertices a and d.
Theorem 1. There is a simple path between every pair of distinct vertices of a connected undirected graph.
Proof: Let u and v be two distinct vertices of a connected undirected graph G = (V, E). Since G is connected, there is at least one path between u and v. Let x 0, x 1, …, xn, where x 0 = u and xn = v, be the vertex sequence of a path of least length. This path of least length is simple. To see this, suppose it is not simple. Then xi = xj for some i and j with 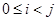 . This means that there is a path from u to v of shorter length with vertex sequence x 0, x 1, …, xi –1, xj, …, xn obtained by deleting the edges corresponding to the vertex sequence xi, …, xj –1.
. This means that there is a path from u to v of shorter length with vertex sequence x 0, x 1, …, xi –1, xj, …, xn obtained by deleting the edges corresponding to the vertex sequence xi, …, xj –1.
A graph that is not connected is the union of two or more connected subgraphs, each pair of which has no vertex in common. These disjoint connected subgraphs are called the connected components of the graph.
Sometimes the removal of a vertex and all edges incident with it produces a subgraph with more connected components than in the original graph. Such vertices are called cut vertices (or articulation points). The removal of a cut vertex from a connected graph produces a subgraph that is not connected. Analogously, an edge whose removal produces a graph with more connected components than in the original graph is called a cut edge or bridge.
Example. Find the cut vertices and cut edges in the graph G.
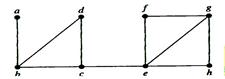
Solution: The cut vertices of G are b, c and e. The removal of one of these vertices (and its adjacent edges) disconnects the graph. The cut edges are { a, b } and { c, e }. Removing either one of these edges disconnects G.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 919; Нарушение авторских прав?; Мы поможем в написании вашей работы!