Пример 2

Таблица 4

Данные о товарообороте предприятий одной из отраслей промышленности.

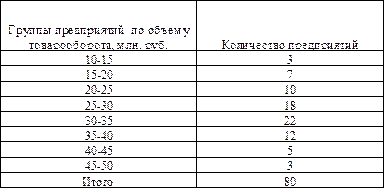
Определить средний объем товарооборота, структурные средние, абсолютные и относительные показатели вариации и насколько фактическое распределение согласуется с нормальным (по показателям формы распределения).

Для расчета показателей построим вспомогательную таблицу.

Таблица 5

Расчетная таблица

Размах вариации:

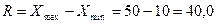млн. руб.

Среднее значение находим по формуле средней арифметической взвешенной:

млн. руб.

В равноинтервальных рядах распределения мода (M_o) и медиана (Me) определяются по следующим формулам:

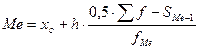
Предварительно выявим интервалы, в которых находится мода и медиана. Наибольшая частота (22) указывает на модальный интервал 30-35 млн. руб. По накопленным частотам определяем, что медиана должна находиться в том же интервале.

В нашем случае их значения равны:

млн. руб.

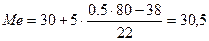млн. руб.

Для определения квартилей используются формулы, аналогичные формуле для расчета медианы. Общая схема их расчета такова: определяется номер для первой и третьей квартилей:

.

По накопленным частотам определяем интервалы, в которых находятся 1 и 3 квартили, соответственно: (20-25) и (30-35).

Величина квартилей определяется по формулам:

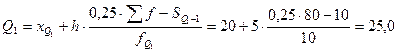млн. руб.

млн. руб.

млн. руб.

Квартильное отклонение:

млн. руб.

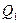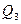где и – соответственно первая и третья квартили распределения.

Среднее линейное отклонение:

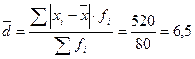млн. руб.

Дисперсия:

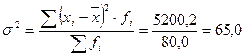
Среднее квадратическое отклонение:

млн. руб.

Рассчитаем относительные показатели вариации.

Коэффициент осцилляции:

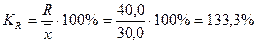
Относительное линейное отклонение:

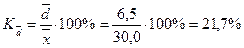
Относительный показатель квартильной вариации:

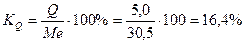
Коэффициент вариации:

Определим показатели формы распределения:

Сформулируем выводы по рассчитанным показателям вариации примера 2, в котором представлен интервальный ряд распределения предприятий по объему товарооборота.

Размах вариации свидетельствует о том, что разница между максимальным и минимальным значением составляет 40 млн. руб. Средний объем товарооборота – 30 млн. руб. Чаще всего встречающееся значение объема товарооборота в рассматриваемой совокупности предприятий – 31,4 млн. руб., причем 50% (40 предприятий) имеют объем товарооборота менее 30,5 млн. руб., а 50% – свыше.

Соотношение характерно для левосторонней асимметрии, при котором большая часть единиц совокупности имеет значение признака ниже модального. Нашему примеру соответствует соотношение 30 млн. руб. < 30,5 млн. руб.< 31,4 млн. руб., что свидетельствует о том, что большая часть анализируемых предприятий имела объем товарооборота ниже, чем его модальное значение (31,4 млн. руб.).

Помимо Mo и Me, количественную характеристику структуры строения вариационных рядов оценивают такие порядковые статистики, как: квартили, квинтили, децили, перцинтили и др.

Степень вариации ряда может быть определена также по формуле квартильного отклонения 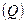, предложенной английским биологом и антропологом Ф. Гальтоном. Это абсолютный квартильный показатель вариации.

Квартильное отклонение, равное 5,0 млн. руб., свидетельствует об умеренной асимметрии распределения, так как в симметричных или умеренно асимметричных распределениях (в рассматриваемом примере ).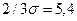

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности. Так, средняя величина колеблемости объема товарооборота предприятий отраслей промышленности составляет: по среднему линейному отклонению - 6,5 млн. руб. (абсолютное отклонение); по среднему квадратическому отклонению - 8,1 млн. руб. Квадрат отклонений индивидуальных значений признака от их средней величины равен 65.

Разница между крайними значениями признака на 33,3% превышает его среднее значение ( = 133,3%).

Относительное линейное отклонение (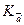 = 21,7%) и относительный показатель квартильной вариации ( 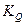= 16,4%) характеризуют однородность исследуемой совокупности, что подтверждает рассчитанный коэффициент вариации, равный 27% ( =27% меньше 30%).

Моментный коэффициент асимметрии 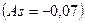в очередной раз подтверждает наличие незначительной левосторонней асимметрии. Основной недостаток моментного коэффициента асимметрии заключается в том, что его величина зависит от наличия в совокупности резко выделяющихся единиц и следовательно его большая (абсолютная) величина будет объясняться доминирующим вкладом в величину центрального момента третьего порядка нетипичных значений, а не асимметричностью распределения основной части единиц.

В связи с тем, что коэффициент осцилляции больше 1 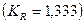, то есть размах вариации на 33 % превышает среднее значение объема товарооборота целесообразно либо исключить из анализа резко отличающиеся единицы совокупности, либо воспользоваться структурными показателями асимметрии.

Структурные показатели (коэффициенты) асимметрии характеризуют асимметричность только в центральной части распределения, то есть основной массы единиц, и в отличии от моментного коэффициента не зависят от крайних значений признака. Воспользовавшись структурным коэффициентом асимметрии К. Пирсона, приходим к выводу, что 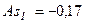свидетельствует в пользу полученных ранее результатов.

Соотношение 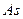и 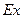с соответствующей средней квадратической ошибкой позволяет утверждать о том, что асимметрия и эксцесс являются несущественными.

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Таблица 6

Дата добавления: 2014-12-23