Теоретичні відомості. Вивчаючи механічні рухи тіл, ми можемо цікавитися тим, яким буде їхнє положення в деякий момент часу (головна задача механіки)

Фазова площина

Вивчаючи механічні рухи тіл, ми можемо цікавитися тим, яким буде їхнє положення в деякий момент часу (головна задача механіки), або тим, коли тіло прийде в деяке певне положення (саме так ставиться задача у сферичній астрономії при прогнозуванні моментів настання затемнень Сонця або Місяця, схоже завдання вирішується при проектуванні виробничого конвеєра).

Проте можна зацікавитися й іншим: загальним характером руху – тим, зокрема, є він періодичним чи ні. Саме такий підхід є характерним для теорії коливань. Наприклад, питання про те, чи може під дією поштовхів сильно розгойдатися міст, вирішується не тим,
наскільки вони сильні, а тим яким є ритм цих поштовхів і скільки часу вони тривають. Інакше кажучи, інтерес уявляє питання про
характер руху, узятого в цілому. Це означає, що ми бажаємо мати таке графічне зображення (діаграму) руху коливальної фізичної системи, яке охоплює усі значення часу t. Бажано, крім того, відобразити на одній діаграмі різноманітні рухи, які може здійснювати тіло.

Найпростішим прикладом механічної коливальної системи є
вантаж на пружині. У такій системі рух відбувається за законом

x = x ₀cos(ωt + φ ₀). (*)

Якщо показати в координатах x, t усі можливі графіки цієї функції з урахуванням різних початкових умов (х ₀ і φ ₀), то, як можна
бачити з рис. 7.10, бажаної мети ми не досягаємо.

Вийшло щось не зовсім розбірливе: графіки перетинаються між собою, до того ж на такій діаграмі можна показати лише частину
кожного графіка в результаті обмеження осі t розмірами малюнка. Крім того, збільшення значень часу t (продовження осі абсцис) ніякої нової інформації про процес не дасть.

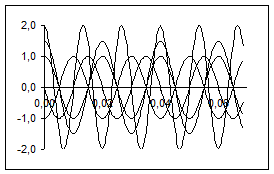
Рис. 7.10

Проте ми отримаємо те, чого бажаємо, якщо візьмемо декартову систему координат і будемо відкладати на осі абсцис зміщення х, а на осі ординат – його похідну, тобто швидкість руху v (ще краще, пропорційну їй величину v / ω). Нагадаємо, що ω має назву циклічна частота, і вона пов’язана зі звичайною частотою v співвідношенням
ω = 2 πv. Ці дві величини x і v / ω повністю характеризують стан тіла, яке здійснює коливання: будь-яка точка на площині змінних х і v / ω зображує стан системи. Таку точку називають зображуючою точкою. Оскільки характеристику стану коливальної системи називають фазою, площина х, v / ω зветься фазовою площиною. Коли вантаж на пружині здійснює коливання, його швидкість змінюється, зображуюча точка переміщується на фазовій площині. Диференціюючи вираз (*), знаходимо:

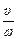= – x ₀ sіn(ωt + j ₀).

Розглянемо тепер систему рівнянь

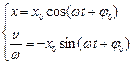
Вони є параметричними рівняннями траєкторії, уздовж якої
переміщається зображуюча точка на фазовій площині, параметром є час t. Параметр легко виключити, підносячи кожне рівняння до квадрату і потім додаючи їх. Це дає:

,

тобто рівняння кола з радіусом, рівним амплітуді x ₀.

На рис. 7.11(а) показане це коло – фазовий портрет гармонічних коливань з постійною амплітудою.

а) б) в)

Рис 7.11

Коливанням з різними амплітудами відповідають концентричні кола з центром у початку координат, як на рис. 7.11(б).

Коливанням з однаковими амплітудами, але з різними фазами відповідає рух зображуючих точок уздовж одного кола, але при цьому в однакові моменти часу зображуючі точки займають різні положення. Різниця фаз дорівнює куту між відповідними радіус-векторами зображуючих точок в однакові моменти часу (рис. 7.11(в).

Розгляд питання про фазовий простір (у даному випадку двомірний) відповідає головному принципу математичного моделювання – принципу множинності математичних моделей. Оскільки при використанні будь-якої конкретної моделі виявляються лише деякі окремі сторони реальності, то для повнішого її вивчення необхідною виявляється сукупність моделей, які дозволяють з різних сторін і з різною мірою деталізації відобразити об’єкт дослідження. Так при вивченні коливальних процесів широко використовуються відомі вам діаграми, які відображають залежність величини, що коливається, від часу, в електротехніці поширеними є так звані векторні діаграми, в загальній теорії коливань до тільки що згаданих підходів додається метод фазових діаграм. Усі ці підходи реалізують різні моделі певних об’єктів (процесів, явищ).

Слід розуміти, що фазовий простір не має нічого спільного з
реальним простором (у разі плоского руху – з координатною площиною ХОY). Зокрема, траєкторія руху зображуючої точки – фазова траєкторія (фазовий портрет) – не є траєкторією руху тіла (матеріальної точки).

Дата добавления: 2015-01-03