Переходные процессы в последовательной RLC-цепи

Рассмотрим два случая переходных процессов в последовательной RLC-цепи:

• последовательная RLC-цепь подключается к источнику постоянной Э.Д.С. Е;

• предварительно заряженный конденсатор разряжается на RLC цепь.

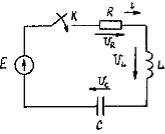
1) При подключении последовательной RLC-цепи кисточнику постоянной Э.Д.С. Е (рис. 6.3.а) уравнение электрического равновесия цепи по второму закону Кирхгофа имеет вид:

U_L+U_R+U_C=E (6.10)

с учетом соотношений

U_R = R•i=R•C•(dU_C/dt);

U_L=L•(di/dt)=L•C•(d²U_C/dt²)

уравнение (6.10) можно записать в виде:

L•C•(d²U_C/dt²) + R•C•(dU_C/dt) + U_C = E (6.11)

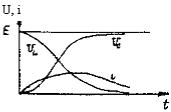
а	б	в
Рис. 6.3

Решение неоднородного дифференциального уравнения (6.11) опреде­ляется характеристическим уравнением: LCp²+RCp+1=0,

которое имеет корни

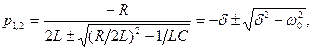(6.12)

где

δ=R/2L - коэффициент затухания,

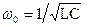- резонансная частота.

В зависимости от соотношения δ² и ω²возможны три основных вида переходных процессов:

а) δ² > ω² или 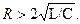Корни характеристического уравнения – отрицательные вещественные. Переходный процесс имеет апериодический характер (рис. 6.3.б).

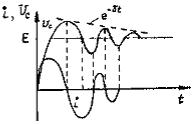
б) δ² < ω² или 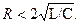Корни характеристического уравнения – комплексные и сопряженные. Характер переходного процесса - колебательный и затухающий (рис. 6.3.в)

в) δ² = ω² или 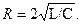Корни характеристического уравнения вещественные и равные p₁=p₂=-R/2L. Характер переходного процесса - апериодический и затухающий (критический случай). Время переходного процесса минимальное.

Для первых двух случаев решение уравнения имеет вид:

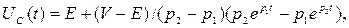(6.13)

где

V=U_C(0) - напряжение на конденсаторе в момент коммутации.

Для случая δ² < ω² уравнение (6.13) приводится к виду:

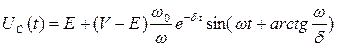, (6.14)

где

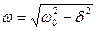- частота затухающих колебаний.

Из уравнения (6.14) следует, что переходный процесс U_c(t) имеет ха­рактер колебаний с угловой частотой ω и периодом Т=2π/ω, которые затухают с постоянной времени τ=2L/R=1/δ.

Для определения величины постоянной времени τ можно использовать огибающую колебательной кривой U_c(t), имеющую форму экспоненты:

exp(-δt)=exp(-t/τ).

Для третьего случая δ=ω₀ решение уравнения (6.11) имеет вид:

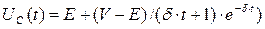. (6.15)

Особенность этого режима состоит в том, что при уменьшении R ниже значения 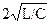переходной процесс становится колебательным.

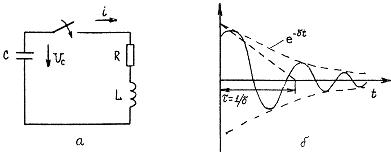
Рис. 6 4

2. При разряде конденсатора на RL-цепь (рис 6.4.а) возможны все три режима, рассмотренные выше и определяемые соотношением величин δ и ω₀. Переходные процессы в этих режимах описываются уравнениями (6.13), (6.14), (6.15) при Е=0. Например, для случая δ<ω₀ уравнение (6.14) при колебательном разряде конденсатора имеет вид:

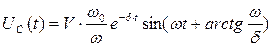(6.16)

Кривая переходного процесса U_c(t) приведена на (рис. 6. 4.б). Огибаю­щей кривой U_c(t) является функция exp(-δt)=exp(-t/τ), которая может быть исполь­зована для определения постоянной времени τ и коэффициента затухания δ=1/τ.

Дата добавления: 2015-01-03