Приклади розв’язання задач. Приклад 1.Півсфера радіусу R=2м освітлюється двома однаковими лампами, які підвішені на висоті 2R над поверхнею землі симетрично відносно півсфери

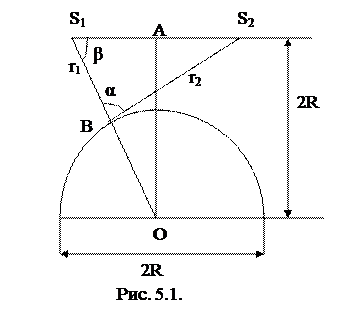
Приклад 1. Півсфера радіусу R=2м освітлюється двома однаковими лампами, які підвішені на висоті 2R над поверхнею землі симетрично відносно півсфери. Відстані між лампи також дорівнює 2R. Визначити освітленість півсфери в точках, які знаходяться на мінімальній відстані від одного з джерел, якщо повний світловий потік кожної лампи дорівнює Ф=1200 лм.

Розв’язання.

Точка В, яка має мінімальну відстань від одного з джерел S₁, знаходиться на лінії S₁О, що з’єднує джерело з центром півсфери. Промені від цього джерела падають на поверхню сфери перпендикулярно.

За формулою (5.6) освітленість в точці В дорівнює

,

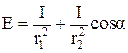де І – сила світла джерел; r₁ і r₂ – відстані джерел від точки В; α – кут падіння променів від джерела S₂.

З урахуванням формули , що надає зв’язок між силою світла та світловим потоком Ф у випадку ізотропного джерела, яким можна вважати лампу,

. (1)

Перевіряємо одиницю вимірювання

.

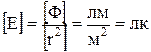Визначаємо r₁, r₂ та cosα.

З прямокутного трикутника 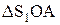за теоремою Піфагора

;

;

.

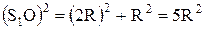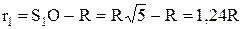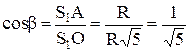З за теоремою косинусів

.

,

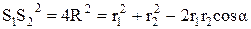звідки .

Підставляємо значення в формулу (1) і отримуємо освітленість Е

лк.

Відповідь: Е = 16,8 лк.

Приклад 2. Промінь світла падає на плоско паралельну пластинку з скла, показник заломлення якого n=1,73, під кутом і=30⁰. Визначити товщину пластинки h, якщо зміщення променя при виході з пластинки становить d = 20мм.

Розв’язання.

Хід променя показаний на рис. 5.2. Виразимо h =AD з прямокутного трикутника АDС:

;

де r – кут заломлення променя світла. За законом заломлення світла (5.12)

.

Звідки ;

=30⁰. Відстань АС знаходимо з : . Тоді

.

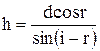м.

Відповідь: м.

Приклад 3. Визначити радіус кривизни R вгнутого сферичного дзеркала, якщо зображення предмета, який знаходиться перед ним на відстані см, збільшене у 5 разів і пряме (k=5).

Розв’язання.

Пряме зображення, отримане за допомогою дзеркала, є уявним. Відповідний хід променів зображений на рис. 5.3.

За формулою сферичного дзеркала (5.20)

, (1)

де, відповідно правилу вибору знаків, а₁ – від’ємне, а₂ – додатне.

Лінійне збільшення у дзеркалі за формулою (5.21) з урахуванням знаків а₁ і а₂ дорівнює

> 0.

Звідки . (2)

З формул (1) і (2) отримуємо ,

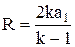. (3)

м.

Відповідь: м.

Примітка. У випадку отримання дійсного оберненого зображення з таким самим за величиною збільшенням k=-5, а₂<0, тобто і за формулою (3) м.

Приклад 4. Між двома плоско паралельними прозорими пластинками поклали дуже тонкий дріт. Дріт паралельний лінії дотику пластинок і знаходиться на відстані а=20 см від неї. При спостереженні у відбитому світлі (λ₀=750 нм) на верхній пластинці спостерігаються інтерференційні смуги. Промені світла падають перпендикулярно до поверхні пластинок. Визначити діаметр D перерізу дроту, якщо на відстані L=1 см спостерігається 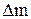=10 світлих смуг.

Розв’язання.

Між пластинками завдяки дроту утворюється повітряний клин. (Рис.5.4а). Тоді діаметр дроту 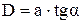(1), де α – заломний кут клина. Визначимо α.

Інтерференційні смуги спостерігаються при малих кутах клина, тому відбиті від верхньої та нижньої поверхонь клина промені 1 і 2 практично паралельні. Різниця ходів цих променів може бути обчислена за формулою (5.29а): .

За умовою інтерференційних максимумів (5.26) (2),

де 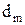– товщина клину в місці, де спостерігається світла смуга з номером m; n – показник заломлення клину (для повітря n=1); r – кут заломлення, який за умовою дорівнює нулю, відповідно ; –додаткова різниця ходи, яка виникає при відбитті другого променя від поверхні нижньої пластинки (середовища з більшим показником заломлення).

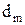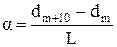Смузі з номером m відповідає товщина повітряного клина , а смузі з номером m+10 – товщина . За умовою десять смуг містяться на відстані L. Тоді шуканий кут α (див. рис. (5.4б)) дорівнює , (3)

де внаслідок малої величини заломного кута .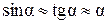

Знаходимо 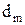і з формули (2) і підставляємо їх до формули (3). Отримуємо

(4)

і за формулою (1)

.

м=7,5∙10^-5м.

Відповідь: =7,5∙10^-5м.

Примітка. Значення кута α за формулою (4) визначається у радіанах.

Правило переводу з радіан у градуси має вид .

Приклад 5. Період дифракційної ґратки d = 2,5 мкм. З якою найменшою кількістю штрихів має бути ґратка, щоб розділити компоненти дублету жовтої лінії натрію, довжини хвиль яких λ₁ = 589,0 нм і λ₂ = 589,6 нм? Визначити найменшу довжину l робочої частини ґратки.

Розв’язання.

За формулою (5.39) роздільна здатність дифракційної ґратки R

. (1)

Мінімальному значенню кількості штрихів N_min відповідає мінімальне значення R_min і максимальне значення порядку спектра m_max, який можна спостерігати за допомогою цієї ґратки, тобто

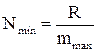. (2)

Мінімальна роздільна здатність, яка є необхідною для розділення компонент дублету, за формулою (1) дорівнює

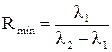. (3)

Число m_max виражаємо з умови максимуму для дифракційної ґратки (5.34), поклавши в ній =1 и λ = λ₂ (вибір у якості λ більшого з двох значень гарантує, що обидві компоненти дуплету з номером m_max будуть спостерігатися). Оскільки m – завжди ціле, за формулою (5.36), отримуємо

. (4)

Підставляємо (3) і (4) в формулу (2). Отримуємо

.

Мінімальна довжина l робочої частини ґратки дорівнює

.

Відповідь: .

Приклад 6. У скільки разів η послаблюється світло, яке проходить через два ніколі, площини яких утворюють кут α=45⁰, якщо в кожному з них втрачається k=10% падаючого на нього світлового потоку?

Розв’язання.

Природне світло інтенсивності І₀ при попаданні на першу призму Ніколя (поляризатор) внаслідок явища подвійного заломлення поділяється на два промені – звичайний і незвичайний. Обидва промені мають однакову інтенсивність 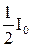і лінійно поляризовані, але в різних площинах. Звичайний промінь внаслідок повного внутрішнього відбиття на межі двох частин ніколя відбивається на внутрішню поверхню призми і поглинається нею. Незвичайний промінь проходить через призму, а його інтенсивність зменшується за рахунок втрат енергії в призмі.

Таким чином, інтенсивність світла, яке пройшло через поляризатор

, (1)

де k – відносна втрата інтенсивності природного світла, яке пройшло через поляризатор.

Далі поляризований промінь інтенсивності І₁ попадає на аналізатор (другий Ніколь) і також поділяється на звичайний і незвичайний промені. Звичайний промінь повністю поглинається призмою, а інтенсивність незвичайного променя І₂ визначається законом Малюса (5.42). Без урахування втрат енергії в другій призмі

, (2)

де α – кут між площинами поляризатора і аналізатора, тобто площинами, в яких прибори пропускають коливання світлового вектора.

З урахуванням втрат інтенсивності в другій призмі, з урахуванням (1) і (2) отримуємо

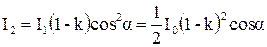. (3)

Звідки .

Підставляємо значення та обчислюємо результат:

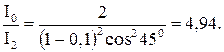
Відповідь:

Приклад 7. Визначити довжину хвилі λ_max, яка відповідає максимумові спектральної випромінювальної здатності волоска лампи розжарювання, площа поверхні якої S=2,5∙10^-5м². Потужність, яка споживається лампою, Р=50 Вт. Вважати волосок лампи сірим тілом, поглинальна здатність якого а = 0,3. Внаслідок теплопровідності іншим тілам передається частка η = 0,2 від енергії, яка споживається лампою.

Розв’язання.

За законом Віна (5.53) , де b = 2,89∙10^-3 м∙К. (1)

Визначимо температури волоска лампи. На розжарювання волоска витрачається доля (1-η) потужності Р, яку споживає лампа. Отже

Р_кор.= .

Відповідно енергетична світність лампи

. (2)

Оскільки лампа є сірим тілом її енергетична світність за формулою (5.51)

а . (3)

За формулами (2) і (3)

а .

Звідки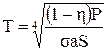

і

.

Перевіряємо одиниці вимірювання:

.

Після підстановки значень знаходимо

м.

Відповідь: λ_max = 8,78∙10^-7м.

Приклад 8. На поверхню літію падає монохроматичне світло (λ = 0,310мкм). Для припинення фотоефекту треба прикласти гальмівну напругу U_г=1,7 В. Визначити роботу виходу електрона з метала та „червону межу” фотоефекту.

Розв’язання.

Записуємо рівняння Ейнштейна для фотоефекту (5.59) з урахуванням зв’язку між частотою фотона ν і довжиною хвилі λ.

,

де с – швидкість світла.

Оскільки навіть найбільш швидкі електрони затримуються електричним полем після проходження в ньому відстані, яка відповідає різниці потенціалів U_г, то їх кінетична енергія безпосередньо після виходу з металу пов’язана з величиною U_г співвідношенням

,

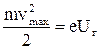Тоді , звідки .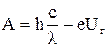

Перевіряємо одиницю вимірювання:

.

Обчислюємо значення
А=6,63∙10^-34∙ =3,70∙10^-19Дж=2,3 еВ.

За формулою (5.60) знаходимо червону межу фотоефекту: .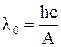

Перевіряємо одиницю вимірювання .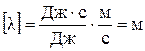

Обчислення: λ₀ = 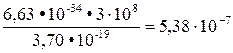м=0,538 мкм.

Відповідь: λ₀ = 0,538 мкм.

Приклад 9. На поверхню цинку падають γ-промені з довжиною хвилі λ=2∙10^-12м. Визначити максимальну швидкість фотоелектронів, які вириваються з поверхня цинку.

Розв’язання.

Порівняємо енергію γ-квантів з роботою виходу електронів з цинку, яка дорівнює А=6,4∙10^-19Дж=4,7 еВ. Енергія фотона γ-променів

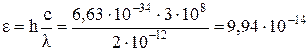Дж.

З урахуванням співвідношення 1МеВ = 1,6∙10^-13 Дж отримуємо: ε = 0,622 Мев >> А, тобто роботою виходу можна знехтувати порівняно з енергією фотона і вважати, що максимальна кінетична енергія електрона дорівнює енергії γ-кванта: Т = ε = 0,62 Мев.

У даному випадку кінетична енергія електрона більша за його власну енергію (енергію спокою) Е₀=m₀c² = 9,11∙10^-31∙(3∙10⁸)²Дж = 8,20∙10^-14 Дж = 0,51 Мев. Тому для обчислення швидкості електрона слід використати релятивістську формулу кінетичної енергії (5.47).

, де β=v/с.

Звідки після відповідних перетворень отримуємо .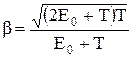

,

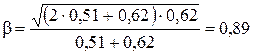звідки м/с = 2,67∙10⁸ м/с.

Відповідь: v = 2,67∙10⁸ м/с.

Дата добавления: 2015-01-03