Проекция вектора на ось, свойства проекций. 3 страница

№49.Три определения непрерывности ф-ции в точке. Классификация точек разрыва.

Ф-ция у=f(х) назыв.непрерывной на интервале (а;b) если она непрерывна в каждой точке этого интервала. Опр. lim_xŠa+0f(x)=f(a), то ф-ция f(х) называется непрерывной в точке а справа. (см.рис.1). lim_xŠb-0f(x)=f(b), то ф-ция f(х) называется непрерывной в точке b слева. Опр: ф-ция у=f(х) назыв. непр.на отрезке [a;b] если она непрерывна в каждой точке интервала (а;b), непрерывна справа в точке а и непрерывна слева в точке b. Если в какой-то точке х_о для ф-ции у=f(х) не выполняется хотя бы одно условие непрерывности, то ф-ция у=f(х) разрывна в точке х_о. В этом случае точка х_о называется точкой разрыва для ф-ции у=f(х). Существуют три вида точек разрыва. 1) если существует предел lim_xŠхоf(x)=a, но он не равен значению ф-ции в точке х_о, тогда точка х_о – точка устранимого разрыва. (см.рис.2). 2) если существует предел ф-ции f(x) при х стремящемся от х_о справа,т.е. lim_xŠхо+0f(x)=f(x_o+0). Существует предел ф-ции f(x) при хŠх_о слева, т.е. lim_xŠхо-0f(x)=f(x_o-0), но они не равны между собой f(x_o+0)≠f(x_o-0), то х_о-точка разрыва 1-го рода (точка скачка). (см.рис.3). Разность f(x_o+0)-f(x_o-0)-величина скачка в точке х_о, т.е. всегда от правостороннего отнимается левосторонний. 3) если хотя бы один из односторонних пределов в точке х_о не сущ. или равен ∞, то точка х_о называется точкой разрыва второго рода. (см.рис.4.). $ lim_xŠхо-0f(x)=a; lim_xŠхо+0f(x)=+∞. Примеры (см.на др.стороне.). 3)-_{(продолжение)} у=^х/_|х|, х≠0 lim_хŠ0+ ^х/_|х|= lim_хŠ0 ^х/_х=1 и lim_хŠ0- ^х/_|х|= lim_хŠ0 ^х/_-х=-1 => по определению, что точка х=0 – точка разрыва 1-го рода. (см.рис.5.).

№50.Непрерывность суммы, произведения и частного непрерывных ф-ций. Непрерывность сложной ф-ции.

Пусть ф-ция у=f(x) задана в некоторой точке хо и некоторой окрестности с центром в точке хо. (см.рис.1.). Придадим аргументу хо некоторое приращение ∆х, т.е. хо+∆х=х, тогда значение ф-ции также изменится. Пусть f(хо)=у. Положим f(хо+∆х)=уо+∆у, тогда ∆у=f(хо+∆х)- f(хо)-приращение ф-ции в точке хо. Опр.:ф-ция у=f(x) называется непрерывной в точке хо, если бесконечно малому приращению аргумента точке хо соответствует бесконечно малое приращение ф-ции в этой точки,т.е. lim∆х0∆у=0 или lim∆х0(f(хо+∆х)- f(хо))=0 или lim∆х0 f(хо+∆х)= f(хо) или limххо f(x)=f(хо) (*),где limххо x=хо. из (*)=>limххо f(x)=f(limххох), т.е. для того чтобы найти предел непрерывной ф-ции в точке хо достаточно подставить в выражение ф-ции вместо аргумента х его значение хо. Пример: докажем: ф-ция у=х2 – непрерывна для любого хо. 1)Возьмём хо. хо=хо+∆х, тогда ф-ция получит приращение ∆у=у(хо+∆х)- у(хо)=(хо+∆х)2-хо2= хо2+2хо*∆х+(∆х)2-хо2=2хо*∆х+(∆х)2. lim∆х0 ∆у= lim∆х0(2хо*∆х+(∆х)2)=0, а это по опр.и означает, что ф-ция y=х2 –непрерывна в любой точке хо. 2)у=sinx, хоR. ∆у=sin(хо+∆х)-sinхо=2sin∆х/2*cos(хо+∆х/2); lim∆х0∆у= lim∆х02sin∆х/2*cos(хо+∆х/2)=0. Аналогично рассматривая каждую осн.элементарную ф-цию можно доказать, что каждая осн.элемент.ф-ция непрерывна в каждой точке, в которой она определена. Теорема1. f1(x) и f2(x) непрерывна в х=хо. α(х)=f1(x)+f2(x) непрерывна в ххо. Док-во: f1(x) непр.в хо=> limххоf1(x)=f1(xо); f2(x) непр.в хо=> limххоf2(x)=f2(xо); limххоα(х)= limххо(f1(x)+f2(x))= limххоf1(x)+limххоf2(x)= f1(xо)+f2(xо)=α(хо)=>α(х)-непрерывна. Аналогично можно жоказать: 1)произведение 2-х непрерывных ф-ций – есть ф-ция непрерывна. 2)частное 2-х непрерывных ф-ций есть ф-ция непрерывная, если знаменатель в рассмотренной точке не равен 0. 3)если ф-ция U=α(x) непрерывна в точке х=хо, а ф-ция f(U) непрерывна в точке U=Uo=α(xo),то сложная ф-ция f[α(x)] будет непрерывна в точке хо. Используя эти теоремы можно доказать теорему2. Можно доказать, что всякая элементарная ф-ция непрерывна в каждой точке, в которой она определена. Примеры (см.на др.стороне).

№51.Непрерывность основных элементарных функций.

Пусть ф-ция у=f(x) задана в некоторой точке х_о и некоторой окрестности с центром в точке х_о. (см.рис.1.). Придадим аргументу х_о некоторое приращение ∆х, т.е. х_о+∆х=х, тогда значение ф-ции также изменится. Пусть f(х_о)=у. Положим f(х_о+∆х)=у_о+∆у, тогда ∆у=f(х_о+∆х)- f(х_о)-приращение ф-ции в точке х_о. Опр.:ф-ция у=f(x) называется непрерывной в точке х_о, если бесконечно малому приращению аргумента точке х_о соответствует бесконечно малое приращение ф-ции в этой точки,т.е. lim_∆хŠ0∆у=0 или lim_∆хŠ0(f(х_о+∆х)- f(х_о))=0 или lim_∆хŠ0 f(х_о+∆х)= f(х_о) или lim_хŠхо f(x)=f(х_о) (*),где lim_хŠхо x=х_о. из (*)=>lim_хŠхо f(x)=f(lim_хŠхох), т.е. для того чтобы найти предел непрерывной ф-ции в точке х_о достаточно подставить в выражение ф-ции вместо аргумента х его значение х_о. Пример: докажем: ф-ция у=х² – непрерывна для любого х_о. 1) Возьмём -х_о. х_о=х_о+∆х, тогда ф-ция получит приращение ∆у=у(х_о+∆х)- у(х_о)=(х_о+∆х)²-х_о²= х_о²+2х_о*∆х+(∆х)²-х_о²=2х_о*∆х+(∆х)². lim_∆хŠ0 ∆у= lim_∆хŠ0(2х_о*∆х+(∆х)²)=0, а это по опр.и означает, что ф-ция y=х² –непрерывна в любой точке х_о. 2) у=sinx, -х_оÎR. ∆у=sin(х_о+∆х)-sinх_о=2sin^∆х/₂*cos(х_о+^∆х/₂); lim_∆хŠ0∆у= lim_∆хŠ02sin^∆х/₂*cos(х_о+^∆х/₂)=0. Аналогично рассматривая каждую осн.элементарную ф-цию можно доказать, что каждая осн.элемент.ф-ция непрерывна в каждой точке, в которой она определена. Теорема1. f₁(x) и f₂(x) непрерывна в х=х_о. α(х)=f₁(x)+f₂(x) непрерывна в хÎх_о. Док-во: f₁(x) непр.в х_о=> lim_хŠхоf₁(x)=f₁(x_о); f₂(x) непр.в х_о=> lim_хŠхоf₂(x)=f₂(x_о); lim_хŠхоα(х)= lim_хŠхо(f₁(x)+f₂(x))= lim_хŠхоf₁(x)+lim_хŠхоf₂(x)= f₁(x_о)+f₂(x_о)=α(х_о)=>α(х)-непрерывна. Аналогично можно жоказать: 1) произведение 2-х непрерывных ф-ций – есть ф-ция непрерывна. 2) частное 2-х непрерывных ф-ций есть ф-ция непрерывная, если знаменатель в рассмотренной точке не равен 0. 3) если ф-ция U=α(x) непрерывна в точке х=х_о, а ф-ция f(U) непрерывна в точке U=U_o=α(x_o),то сложная ф-ция f[α(x)] будет непрерывна в точке х_о. Используя эти теоремы можно доказать теорему2. Можно доказать, что всякая элементарная ф-ция непрерывна в каждой точке, в которой она определена. Примеры (см.на др.стороне).

№52. Определение производной, её механический и геометрический смысл. Уравнение касательной к нормали к графику ф-ции.

Пусть у=f(x) определена в некотором промежутке X. (см.рис.1.). Дадим аргументу х нек-ое приращение ∆х, получим новое значение аргумента х+∆х. Точка х+∆хÎХ. Тогда значение ф-ции получит приращение ∆у=f(х+∆х)-f(x). lim_∆хŠ0^∆у/_∆х= lim_∆хŠ0^{f(x+∆x)-f(x)}/_∆х. Опр: если, существует предел отношения приращения ф-ции к приращению аргумента при условии, что приращение аргументаŠ0, то этот предел называется производной ф-ции в данной точке и обозначается f'(x), т.е. f'(x)= lim_∆хŠ0^{f(x+∆x)-f(x)}/_∆х.-опр.произв. Обозн.у';у'_х;f'(х);^dy/_dx. у'(а);у'|_х=а-знач.произв. в х=а. Операция нахождения произв.ф-ции в точке назыв. дифференцируемой. Пользуясь опр.найти произв.(см.№2 на др.стороне). Выясним.геом.смысл.произв. (см.рис.2.). Если М₁ не ограничена по кривой, приближается у точке М, то секущая (М;М₁) принимает различные положения. Если при не ограниченном приближении точки М₁ по кривой точки М с любой стороны секущая стремится занять положение определённой прямой МТ, то прямая МТ назыв.касат. прямой к точке М. (см.рис.3.). Рассм. у=f(x). Пусть точка М₀ имеет корд. (х_о;f(x_o)). Если аргументу х_о придать приращение ∆х, то на графики ф-ции получим точку М(х_о+∆х;f(x_o+∆х)). Проведём секущую М₀М и обозн. угол между положит.оси Ох и секущей. tgφ=^∆у/_∆х. Если теперь устремить точку М по кривой к М₀, то секущая М₀М будет вращаться вокруг точки М₀. И угол φ будет изменяться при изменении ∆х. Если при ∆хŠ0 угол φ будет стремится к некоторому пределу α, то прямая проходящая через точку М₀ и образующая с положительным направлением оси Ох угол α будет искомой касательной. Найдём её угловой коэффициент tgα. tgα=lim_∆хŠ0tgα=lim_∆хŠ0^∆у/_∆х=у'(x), у'(х)=tgα., т.е. значение производной у'(х) при данном значении аргумента х равен тангенсу угла, образованного касательной к графику ф-ции в данной точке с положительным напр.оси Ох. (пример№2.см.на.др.стороне.).

№54.Теорема о непрерывности дифференцируемой ф-ции. Пример непрерывной, но недифференцируемой ф-ции.

Если ф-ция у=f(х) имеет производную в точке х= x_o, т.е. если сущ. предел отношения lim_∆хŠ0^∆у/_∆х= lim_∆хŠ0^{f(x+∆x)-f(x)}/_∆х, то ф-ция у=f(х) называется дифференцируемой в точке х_о. Теорема: если ф-ция у=f(х) дифференцируема в точке х= x_o,то она непрерывна в точке х_о. Док-во: по усл.$ lim_∆хŠ0^∆у/_∆х=f'(x_о)=> ^∆у/_∆х=f'(x_о)+α(∆х), где f'(x_о)Š0 при ∆хŠ0=>∆у=f'(x_о)*∆х+α(∆х)*∆х=>,что если ∆хŠ0, то ∆уŠ0. А это по опр.означает, что ф-ция у=f(x) непрерывна в точке х_о. Обратное утверждение не верно, т.е. если ф-ция непрерывна в точке х_о, то отсюда не следует, что она дифференцируема в этой точке. Пусть f(x)={x,0≤x≤1; 2x-1, 1≤x≤2. Эта ф-ция при х=1 не имеет производной, хотя и непрерывна в этой точке. Пусть ∆х>0. lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0^{f(1+∆x)-f(1)}/_∆х= lim_∆хŠ0^{2(1+∆x)-1-1)}/_∆х= lim_∆хŠ0^2∆x/_∆х=2.(см.рис.1.). Пусть ∆х<0. lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0^{f(1+∆x)-f(1)}/_∆х= lim_∆хŠ0^1+∆x-1)/_∆х= lim_∆хŠ0^∆x/_∆х=1, т.е. рассматриваемый предел зависит от того каков знак ∆х. А это означает, что в точке х=1 ф-ция f(x) производной не имеет. С другой стороны эта ф-ция непрерывна в точке х=1. Если ∆х>0,то ∆у=2∆х, а если ∆х<0,то ∆у=∆х=>при ∆хŠ0, ∆уŠ0, т.е. у=f(x) непрерывна в х=1. из теоремы следует, что в точках разрыва ф-ция не может иметь производной. Примеры вычисления производной.: 1)степенная ф-ция у=х^α,αÎR,x>0. Дадим аргументу х приращение ∆х и получим х+∆х. ∆у=у(х+∆х)-у(х)=(х+∆х)^α-х^α=х^α(1+^∆х/_х)^α-х^α= х^α((1+^∆х/_х)^α-1). у'=lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0(х^α(1+^∆х/_х)^α-1)/_∆х= х^αlim_∆хŠ0^α*∆х/х/_∆х= х^αlim_∆хŠ0^α/_х=α*х^α-1. (х^α)'=α*х^α-1. -эта формула верна для любого х из области опр.ф-ции. (х)'=1(α=1); (¹/_х)'=-¹/х²(α=-1); (√х)'=¹/_2√х(α=½). (ост.примеры см.на др.стороне.).

№56. Производные тригонометрических функций.

Производная от y=sinx, это y’=cosx. Дадим аргументу x приращение ∆x; тогда 1) y+∆y=sin(x+∆x); 2) ∆y=sin(x+∆x)-sinx=2sin ;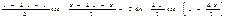

3) 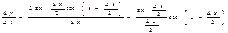; 4) 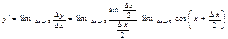, но так как , то =cosx. Последнее равенство получается на том основании, что cosx есть непрерывная функция. Так же y=cosx y’=-sinx. Производная от y=tgx, равна 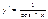. По правилу дифференцирования дроби получаем: . Так же y=ctgx, равен .

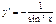№57. Производная степенной и показательной функций.

Производная от (показательная функция) функции a^x, где а > 0, равна a^xlna, т.е. y=a^x, равна y’=a^xlna. Логарифмируя равенство y=a^x, получим: lny=xlna или y’=a^xlna. Если оснавание а=е, то lne=1 и мы получим y=e^x, y’=e^x. Производная от (степенная функция) xⁿ, где n – любое действительное число, равна nx^n-1. Пусть x > 0. Логарифмируя данную функцию, будем иметь: lny=nlnx. Дифференцируем обе части полученного равенства по х, считая у функцией от х: 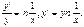Подставляя сюда значение y=xⁿ, окончательно получаем: y’=nx^n-1. Эта формула верна и для x < 0, если только xⁿ имеет смысл.

№58. Производная логарифмической функции. Логарифмическое дифференцирование, производная степенно-показательной функции.

Производная от log_ax, равна 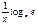или . Если ∆y есть приращение функции y=log_ax, соответствующее приращению ∆x аргумента x, то y+∆y=log_a(x+∆x); ∆y=log_a(x+∆x)-log_ax= . Помножим и разделим на x выражение, состоящее в правой части последнего равенства 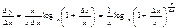. Обозначим величину через α. Очевидно, при и данном x. Следовательно, , но как известно 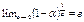. Если же выражение, стоящее под знаком логарифма, стремится к числе e, то логарифм этого выражения стремится к log_ae (в силу непрерывности логарифмической функции). Поэтому окончательно получаем: . Заметив, что , полученную формулу можно переписать так: .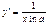

№59.Производные обратных тригонометрических функций.

1)Рассмотрим ф-цию y=arcsinx;-1≤x≤1.Обратной этой ф-ции явл. x=siny (-π/2≤y≤π/2) Причём производная обратной ф-ции сущ. x’(y)=cosy;≠0;для любого у из(-π/2;π/2) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=1/cosy=1/cos(arcsinx)=1/√(1-sin²(arcsinx))=1/√(1-x²) (arcsinx)’=1/√(1-x²) Аналогично ( arccosx)’= -1/√(1-x²) xε(-1;1) 2)y=arctgx x xε(-∞;∞)Обратная x=tgy -π/2≤y≤π/2 Производная обратной ф-ции сущ. x’(y)=1/cos²y≠0 для любого у ε(-π/2;π/2)) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=cos²y=cos²(arctgx)=1/1+tg²(arctgx)=1/1+x² (arctgx)’=1/1+x² xε(-∞;∞) Аналогично (arсctgx)’= -1/1+x²) (с графиками).

№60.Гиперболические ф-ции и их производные.

Ф-ция y=e^x-не явл. ни чётной,ни нечётной,но её можно представить в виде суммы двух слагаемых из которых одно:чётная,второе-нечётная ф-ция e^x=(e^x+e^-x)/2+(e^x-e^-x)/2

(e^x+e^-x)/2=chx-гиперболический cos (чётная)

(e^x-e^-x)/2=shx-гиперболический sin(нечётная)shx/chx=thx

chx/shx=cthx

Св-ва гиперболических ф-ций напоминают св-ва тритгонометрпических ф-ций

ch²x-sh²x=1; ch²x+sh²x=ch2x; 2shx *chx=sh2x

Найдём произв.от тригонометрич.ф-ций: (shx)’=chx; (chx)’=shx;thx=1/ch²x;

(cthx)’= -1/sh²x

№61.Производные неявных и параметрических ф-ций.

Неявн. Пусть знач.x и y связаны некоторым ур-ем F(x;y)=0(1)Если ф-ция y=f(x)определена на интервале(ab),такова что ур-е(1)при подстановке в него вместо y выраж.f(x)обращается в ождество относительно x,то ф-ция y=f(x)есть неявная ф-ция,определёная ур-ем(1) Но не всякую неявно заданную ф-цию можно представить явно. Например y-x-siny=0

не всякую явно заданную ф-цию можно представить неявно При вычисл.знач. произв.неявной ф-ции при данном знач.ар-та,нужно знать ещё и знач.ф-ции y,при данном знач.аргумента Парам. {x=α(t); y=λ(t)(1)T1≤t≤T2 Каждому значению t соответствуют значения x и y.Если рассматривать x и y как координаты точки на плоскости XOY,то каждому значению t будет соответствовать определённая точка на плоскости.Когда t изменяется от T1 до Т2,то эта точка на пл-ти описывает некоторую кривую.Ур-я(1)называются параметр.ур-ями этой кривой,t параметром.А способ задания кривой ур-ями(1)называется параметрическим. Пусть ф-ция x=α(t)имеет обратную t=Ф(x),тогда y явл.сложной ф-цией от x.y=α[Ф(х)]Таким образом ур-я (1)определяют у как ф-цию от х, и говорят что эта ф-ция у(х)задана параметр. Найдём произв.ф-ции заданой ур-ями (1).Предположим,что α(t),λ(t)имеют произв.,кроме того ф-ция х=λ(t),имеет обратную t=Ф(х),которая также имеет производную,тогда ф-цию у=f(x)можно рассматр. Как сложную ф-цию у=λ[Ф(х)],t=Ф(х)-промежуточный аргумент y'(x)=y’(t) *t’(x)по правилу дифф. Обратной ф-ции. y’(x)=y’(t)/x’(t) или y’(x)=λ’(t)/α’(t).

№62.Дифференциал ф-ции, его геометрический смысл.

Пусть ф-ция y=f(x)дифф.на отр.ab,существует f’(x)=lim(∆xà0)∆y/∆x => ∆y/∆x=f’(x)+α,где αà0. ∆y=f’(x)∆x+α∆x (1)Т.к. в общем случае f’(x)≠0,то при постоянном х и переменном ∆х→0,первое слагаемое в рав-ве(1)есть б.м.в.,того же порядка что ∆х.Авторое слагаемое-б.м.в. более высокого порядка чем ∆х lim(∆x→0)α∆x/∆x=0. Таким образом приращение ф-ции ∆у состоит из двух слагаемых из которых 1-ое –главная часть приращения относительно ∆х f’(x)∆x-называют дифференциалом ф-ции и обозначают dy или df(x) dy= f’(x)∆x По опр. Полагают,что дифф. Переменного dx=∆x Это опр. Оправдано,т.к.если y=х,то dy=dx=∆x dx=∆x dy=f’(x)dx,отсюда f’(x)=dy/dx.Т.е. произв. можно представить как отношение дифференциала ф-ции к дифф. арг-та Из (1)=> ∆y=dy+α∆x Т.е. приращение ф-ции отлич.от диф. На б.м.в.более высокого порядка чем ∆х α∆х-б.м.в.более высокого порядка,чем dy.Поэтомув приближённых вычислениях пользуются равенством ∆y≈dy f(x+∆x)≈f(x)+f’(x)∆x-формула для приближ.вычислений.Правила относящиеся к производным сохр. и для дифференциалов Пример y=tg²xdy=2tgx*1/cos²x*dx

Геометр.смысл.дифференциала Рассмотрим y=f(x)и соотв. ей кривую (рисунок) NT=MNtgα=∆xf’(x)=dy таким образом, дифф.ф-ции y=f(x) соответств.данным значениям х и ∆х равен приращению ординаты касательной к гр-ку ф-ции f(x) в точке х.

№63.Применение дифференциала к приближённым вычислениям.

Пусть ф-ия y=f(x), xÎ[a;b] дифференцируема на [a;b]. Это значит, что существует f’(x)=lim_DX®0 Dx/DyÞDx/Dy=f’(x)+a, где a®0 при Dх®0; Dy=f’(x)Dх+aDх. Т.к. в общем случае f’(x)¹0, то при постоянном х и переменном Dх®0 первое слагаемое в правой части равенства Dy=f’(x)Dх+aDх есть бесконечно малая величина того же порядка, что и Dх. А второе слагаемое есть б.м.в. более высокого порядка чем Dх, т.к. lim_DX®0 aDx/Dх=lim_DX®0 a=0. Таким образом приращение ф-ии Dу состоит из двух слагаемых, из которых первое при f’(x)¹0, есть главная часть приращения, линейная относительно Dх. Это слагаемое f’(x)Dх наз. дифференциалом функции и обозначают dy=f’(x)Dx. По опрнделению полагают, что дифференциал независимой переменной равен приращению этой переменной. Это определение оправдано т.к. у=х, dy=dx=1 Dх; dx=DхÞdy=f’(x)Dх. Отсюда можно выразить f’(x)=dy/dx, т.е. производную можно представить как отношение дифференциала ф-ии к дифференциалу аргумента. Таким образом из Dy=f’(x)Dх+aDх следует Dy=dy+aDх, т.е. приращение ф-ии отличается от её дифференциала на б.м.в. более высокого порядка чем Dх, кроме того aDх при f’(x)¹0 является б.м.в. более высокого порядка чем dy и lim_DX®0 Dy/dy=lim_DX®0 (dy+aDx)/dy=lim_DX®0 1+aDx/dy=1+ lim_DX®0 aDx/f’(x)Dx=1+0=1. Поэтому в приближённых вычислениях пользуются равенством Dу» dy, f(x+Dx)–f(x)» f’(x)Dx, f(x+Dx)» f(x) + f’(x)Dx.

Дата добавления: 2015-01-03