Проекция вектора на ось, свойства проекций. 2 страница. Переменной величиной называется величина, которая принимает различные численные значения

Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной. В математике постоянная величина часто рассматривается как частный случай переменной, у которой все численные значения одинаковы. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y есть функция от x или, в символической записи, y=f(x), y=φ(x), и т.п. Способы задания функции. 1) Аналитический. 2) Графический. 3) Табличный. 4) Словесно.

№36. Основные элементарные функции их графики.

Если к каждому значению переменной «х» из некоторой области соответствует одно определенное значение «у», то это называется функция от переменной «х» у=f(х). х- независимая переменная или аргумент. Зависимость между «х и у» называется функциональной буквой «f» в символической записи функция означает, что над «х» надо произвести некоторые операции, чтобы получить «у». Совокупность значений «ч» для которых определяется значение функции «у» в силу правила f(x) называется областью определения функции. Они бывают: 1) степенная y=x^α α€R x>0. 2)показательная y=a^x a>0 x€R a≠1. 3) Тригонометрические y=sinx y=cosx y=secx и т.д. 4) Логарифмические y=log_ax a>0, a≠1, x>0. 5) Обратные тригонометрические y=arcsinx, y=arccosx, и т.д.

№37. Четные и нечетные функции. Периодические функции. Свойства четной функции y=│x│.

Если исследуемая функция при изменении знака аргумента значение функции не изменяется то эта функция четная, f(-x)=f(x),а если при изменении знака аргумента знак меняется то она нечетная, f(-x)=-f(x). Функция y=f(x) называется периодической, если существует такое постоянное число C, от прибавления (или вычитания) которого к аргументу x значение функции не изменяется: f(x+C)=f(x). y=│x│ (рис) f ’(0) не существует. Определенной касательной провести нельзя. x=0 –min, y(0)=0, y(x)>y(0) при 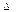x>0, при 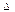x<0.

№38.Определение предела функции в точке, геометрическая интерпретация.

Опр:пусть ф-ция y=f(x) определена в нек-ой окрестности точки а. число b называют пределом ф-ции f(x) при хŠ∞ если для любого числа e>0 сущ.чмсло δ зависящее от e>0,такое,что для всех х отличных от “а”и удовлетворяющих нер-ву |х-а|<δ будет выполняться нер-во |f(x)-b|<e. y=f(x) b=lim_xŠa f(x),если для -e>0 сущ.δ(e)>0, -х≠а,|х-а|<δ,=>|f(x)-b|<e; 0<|x-a|<δ. Пусть f(x)Šb при хŠа. Т.к. из нер-ва |х-а|<δ=>|f(x)-b|<e,то это значит, что для всех х отстоящих от точки а не далее чем на δ точка М графика ф-ции f(x) лежит в полосе шириной 2e ограниченной двумя горизонтальными прямыми (см.рис.1). Опр:если ф-ция yŠb₁ при xŠa, x<a,то limf(x)=b₁ при хŠа-0(см.рис.2.). В этом случае число b₁ назыв.пределом ф-ции f(x) в точке х=а слева. Если х>0, то lim_xŠa+0 f(x)= b₂, а число b₂ назыв.пределом ф-ции f(x) x=a справа. Пределы слева и справа назыв.односторонними пределами (см.рис.3). Можно доказать, что для того чтобы предел ф-ции f(x) при хŠа был=b необходимо и достаточно, чтобы сущ.предел f(x). lim_xŠa f(x)= bÛсущ. lim_xŠa-0 f(x)= b и lim_xŠa+0 f(x)= b. При определении предела ф-ции в точке не требуется, чтобы ф-ции y=f(x) была определена в точке х=а. При нахождении предела ф-ции рассмотр.знач.ф-ции в окрестности точки а. Число b назыв.lim ф-ции f(x)при xŠ∞ если для любого сколь угодно малого “+”числа e сущ.число N=0,такое что для всех |х|>N выполняется нер-во f(x)-b<e (см.рис.4.).

№39.Бесконечно малые (б.м.) и их свойства.

Опр:ф-ция y=a(x) назыв.б.м. при хŠа, если lim_хŠаa(x)=0. Основные св-ва. Алгебраическая сумма любого конечного числа бесконечно малых ф-ций есть бесконечно малая ф-ция. 1)пусть U(x)= a(x)+b(x), где lim_хŠаa(x)=0 и lim_хŠаb(x)=0,т.е.нам надо доказать, что для любого e>0 сущ.число δ>0, такое что для всех х удовл.нер-ву 0<|х-а|<δ будет выполнится нер-во |U(x)-0|<e или |U(x)|<e. Докажем: т.к. lim_хŠаa(x)=0=>то по определению это значит,что для любого e>0 сущ.δ₁-окрестность точки а, в кот-ой выполняется нер-во |a(х)|<e/2. Т.к. lim_хŠаb(x)=0,то для выбранного e сущ.δ₂-окрестность точки а, в кот-ой выполняется нер-во |b(х)|<e/2. Обозн. через δ наименьшее из чисел δ₁ и δ₂. δ=min|δ₁,δ₂|, тогда в δ окрестности точки “а” будет выполнятся нер-во: |U(x)|=|a(x)+b(x)|≤|a(x)|+|b(x)|<e/2+e/2=e, т.е.|U(x)|<e=>lim_xŠaU(x)=0,т.е.U(x)-бесконечно малая ф-ция. Аналогичное док-во для случая когда lim_хŠаa(x)=0 и lim_хŠаb(x)=0. 2)Произведение б.м.ф-ции при хŠа (или хŠ∞). На ограниченную ф-цию есть б.м.ф-ция. Пусть lim_хŠаa(x)=0=>,что для любого e>0 сущ.δ₁-окрестность точки а, в кот-ой выполняется нер-во |a(х)|<e/М,где M>0. y=f(x)-ограниченная, то по определению это означает, что сущ.такое δ₂-окрестность точки а, в кот-ой выполняется нер-во |f(x)|<M,M>0. Обозн.через δ наименьшие из чисел δ₁,δ₂,тогда в δ-окрестности точки “а” будет выполняться нер-во: |a(x)*f(x)|=|a(x)|*|f(x)|<eM/M=>a(x)*f(x)-бесконечно малая величина. 3)a(x)/f(x)-бесконечно малая ф-ция a(х) и ф-ция lim_хŠаf(x)=b≠0-есть бесконечно малая ф-ция. Дейст-но пусть lim_хŠаa(x)=0,а lim_хŠаf(x)=b≠0=>1/f(x)-ограниченная ф-ция, а отсюда следует, что a(x)/f(x)=a(х)*1/f(x)=беск.алая ф-ция. 4)произведение любого конечного числа бесконечно малое есть б.м. 5)произвед.б.м.ф.на const.есть б.м.ф. 6)если a(х)-б.м.в. при хŠа (или хŠ∞), то 1/a(x)-б.б.в.при хŠа (или хŠ∞). 7)если при lim_хŠаf(x)=b, то f(x)=b+a(x),где lim_хŠаa(x)=0.

№40.Теорема о разности между переменной величиной и её пределом.

Опр: число а назыв.пределом переменной величины х если для любого сколь угодно малого положительного числа e можно указать такое значение переменной х, начиная с которого все последующие знач.переменной будут удовлетворять след.нер-ву: |х-а|<e;-e<x-a<e;a-e<x<a+e (см.рис.1.). а=limх при хŠа. Пример:х₁=1+1;х₂=1+¹/₂;х₃=1+¹/₃;……;х_n=1+¹/_n… Докажем пользуясь опр.,что lim_x→∞x_n=1: Рассм. |x_n-1|<e;|1+¹/_n-1|<e;¹/_n<e;n>¹/_e.=>,что все члены последовательности с номерами большими чем ¹/_e будут удовлетворять след.нер-ву: |x_n-1|<e.ч.т.д. Замечания: 1)очевидно, что предел постоянной величины=самой постоянной,т.е. limc=c,где c=const. Действит.возьмём -e>0 и рассм. |х-с|=|с-с|=0<e,для -e>0. 2)переменная величина не может иметь двух различных пределов. Действит-но limx=a и limx=b,a≠b.пусть для определённости a<b,тогда согласно определению если limx=a и limx=b,то сущ.знач.х, начиная с кот-ого все послед.знач.удовлетворяют нер-ву. limx=a и limx=b; |x-а|<e и |x-b|<e, а это невозможно если взять e<(b-a)/2 (см.рис.2). …,если y переменой величины сущ.,то этот предел единственный. Говорят,что переменная хŠ∞ если для каждого наперёд заданного положит-но числа М сущ.такое знач.х, начиная с кот-ого все послед.знач.х удовлетворяют нер-ву |х|>M.если переменная хŠ∞, то её назыв.бесконечно большой переменной величиной (б.м.в.).Пример:х₁=-1,х₂=2,х₃=-3…х_n=(-1)ⁿ*n-эта переменная величина будет бесконечно малойсм .(рис.3). Говорят,что переменная величина хŠ+∞,если для -М>0 все послед.знач.х удовлетворяют нер-ву. Пример: х₁=1,х₂=2…х_n=n… (см.рис.4.). Говорят,что переменная хŠ-∞,если для любого M>0 все послед.знач.х начиная с нек-ого удовл.нер-ву.x<-M (см.рис.5). Пример. х₁=-1,х₂=-2,х₃=-3…х_n=-n…

№42.Бесконечно большие ф-ции,их связь с бесконечно малыми.

Опр. ф-ция f(x)назыв.бесконечно большой(б.б.) при хŠа (т.е.Š∞ при хŠа), если для любого числа М>0, сущ.число δ>0 для всех х удовл.нер-ву 0<|x-a|<δ будет выполняться |f(x)|>M,т.е. lim_xŠaf(x)=∞,если -M>0 сущ.δ>0, такое что х-; 0|х-а|<δ;|f(x)|>М .(см.рис.1.). В этом случае пишут lim_xŠaf(x)=∞ или f(x)Š∞ при хŠа. если ф-ция f(x) явл.б.б. и при этом сохраняется только “+” или только “—”,знач.,то в этом случае пишут lim_xŠaf(x)=+∞ или lim_xŠaf(x)=-∞. Докажем: lim_xŠ1 1/(1-x)²=+∞. Берём любое число M>0 и рассм.|f(x)|=+∞, |f(x)|>M; 1/(1-x)²>M; (1-x)²<1/M; |1-х|<√1/М=δ=>что в качестве δ можно взять √1/М. Для любого х, отличного от 1 наша ф-ции будет>0,т.е.ф-ция f(x)-б.б. и f(x)>0=>предел нашей ф-ции=+∞,т.е. -х≠1 1/(1-х²)>0=>f(x)-б.б.в. и f(x)>0 =>lim_xŠ1f(x)=+∞. Если ф-ция f(x)Š∞ при хŠ∞, то пришут:lim_xŠ∞f(x)=∞. Пример. lim_xŠ∞х²=+∞; lim_xŠ-∞х³=-∞; Замечания:ф-ция y=f(x) при хŠа ил при хŠ∞ может не стремится ни к конечному, ни к бесконечному пределу. 1)y=sinx,xÎR при хŠ∞ y=sinx не имеет предела. 2)ф-ция y=sin1/x, x≠0 при хŠ0 не имеет предела. Опр. ф-ции y=f(x) назыв.ограниченной в нек-ой области изменения х если сущ.число M>0, такое что для всех х из этой области |f(x)|≤M. y=sinx-ограничена, т.к. |sinx|≤1=M. Опр:ф-ция y=f(x) назыв.ограниченной при хŠа если существуют окрестность с центром в точке А, в кот-ой ф-ция f(x) явл.ограниченной. Опр. ф-ция y=f(x) назыв.ограниченной при хŠ∞, если сущ.число N>0, такое что для всех |х|>N ф-ция ограничена. Теорема: если lim_хŠaf(x)=b, где b-конечное число, то f(x) ограничена при хŠа. Док-во. из равенства lim_хŠaf(x)=b=>для любого e>0 сущ.δ>0, такое что для всех х, удовлетворяющих нер-ву 0<|х-а|<δ будет выполняться нер-во |f(x)-b|<e,т.е. в заданной δ окрестности точки а. |f(x)|-|b|≤|f(x)-b|<e; |f(x)|-|b|≤e; |f(x)|<e+|b|=>ф-ция f(х) ограничена в δ окрестности точки а. Замечание:из определения ограниченной ф-ции следует, что если ф-ция f(x) явл.б.б. (т.е.если lim_xŠaf(x)=∞ или lim_xŠ∞f(x)=∞), то она не является ограниченной. Обратное не верно: неограниченная ф-ция может и не быть б.б. Пример. y=xsinx,xÎR-неограниченная,т.к. для любого М>0 найдётся х |хsinx|>M,но эта ф-ция не явл.б.б.,т.к.y=0 при х=0,p,2p…

№43.Свойства функций, имеющих конечный предел.

Пусть xŠa или xŠ∞. Теорема 1:предел алгебраической суммы конечного числа переменных=сумме пределов этих переменных,т.е. lim(U₁+U₂+…+U_n)=limU₁+limU₂+…+limU_n. Док-во: пусть предел U=а и пусть limV=b, тогда по св-ву 7(теорема о связи) имеем U=a+a и V=b+b-бесконечно малые величины. Р ассм. переменную величину: U+V=(a+a)+(b+b)=(a+b)+(a+b)=>а это по теореме по связи означает: lim(U+V)=(a+b)=limU+limV. Пример:lim_xŠ∞(x²+2x)/x²=[∞/∞] =lim_xŠ∞(1+²/_x)= lim_xŠ∞1+lim_xŠ∞²/_x =1+0=1. Теорема 2: предел произведения конечного числа переменных=произвед.пределов этих переменных,т.е. lim(U₁*U₂*…*U_n)=limU₁*limU₂*…*limU_n. Док-во:пусть limU=а=>по св-ву(7) U=a+a,где a-б.м.в.; limV=b=>по св-ву(7) V=b+b,где b-б.м.в. Рассм. U*V=(a+a)*(b+b)=ab+ab+ba+ab= число+б.м.в.+б.м.в.+б.м.в.,т.е. переменную величину U,V мы смогли представить в виде суммы нек-го числа аb и б.м.в., а это по теореме о связи означает, что lim(U*V)=a*b=limU*limV, теорема доказана. Следствие: постоянный множитель можно выносить за знак предела. Пусть limU=a, a c=const=>limC=C. Рассм. lim(C*U)=limC*limU=C*limU=C*a. Пример: lim_xŠ25x³=5lim_xŠ2x²=5*8=40. Теорема 3: предел частного 2-х ф-ций =частному пределов этих переменных если предел знаменателя отличен от 0,т.е. lim(U/V)=limU/limV,где limV≠0. Док-во: пусть limU=а=> U=a+a,где a-б.м.в.; limV=b=> V=b+b,где b-б.м.в. Рассм. U/V=(a+a)/(b+b)=a/b+((a+a)/(b+b)-a/b)=a/b+((ab+ab-ab-ab)/b(b+b)) =a/b+((ab-ab)/ b(b+b))-(б.м.в.)=>lim(U/V)=a/b=limU/limV-ч.т.д. Пример: 1),2),3)-(см.№1на др.стороне). Теорема 4: если между соответствующими значениями 3-х ф-ций: U(x), Z(x),V(x) выполняется нер-во U≤Z≤V и при этом ф-ции U и VŠк одному и тому же limb при хŠa или xŠ∞, то и ф-ция Z при хŠa или xŠ∞ будет стремится к тому же самому limb. Док-во: пусть хŠa. По усл: U≤Z≤V, тогда из этого нер-ва =>U-b≤Z-b≤V-b. По усл: lim_хŠaU=b=>(по опр.) это означает, что для любого ε>0 cущ.окрестность точки а в кот-ой будет выполняться нер-во |U-b|<ε. Или –ε<U-b<ε (1). По усл: lim_хŠaV=b=> для выбранного ε сущ.окрестность точки а в кот-ой выполняется нер-во: |V-b|<ε. –ε<V-b<ε (2), тогда в меньшей из этих 2-х окрестностей будут выполняться оба нер-ва (1) и (2). (см.№2 на др. стороне). Теорема 5: если при хŠa или xŠ∞ ф-ция y принимает неотрицат.знач-ия а имеет своим пределом число b, то b≥0,т.е. y≥0, lim_{хŠaилиxŠ∞}y=b=>b≥0. Док-во: предположим противное: пусть b<0, тогда |y-b| будет ≥|b|,т.е. модуль разности |y-b| больше положительного числа модуль |b|,т.е. модуль разности не стремится к 0 при хŠa или xŠ∞=> число b не может быть пределом ф-ции y, что подтверждает условие=>наше предположение не верно и b≥0. Аналогично доказывается: y≤0, lim_{хŠaилиxŠ∞}y=b=>b≤0. Теорема 6: если между соответствующими знач-ми 2-х ф-ций U и V выполняется нер-во U(x)≤V(x), то limU≤limV при хŠa или xŠ∞. Док-во: по усл: V-U≥0. Рассм. lim(U-V)≥0, но limV-limU≥0=>limV≥limU.ч.т.д.

№45.Первый замечательный предел.

Ф-ция y=^sinx/_x при xŠ0 не определена в точке х=0. найдём её предел при xŠ0 (см.рис.1). Пусть 0<x<^π/₂. S_∆OMA<Sсект. AMO<S_∆OCA. Scект.=πR²/_2π*x,т.е. ½R*|MB|<½R²*x<½R*|CA|; ½sinx<½x<½tgx|*2; sinx<x<tgx|:sinx; 1<^x/_sinx<¹/_cosx; cosx< ^sinx/_x<1(*), т.к. lim_xŠ0cosx=1; lim_xŠ0=1, то по теореме о пределе промежуточной переменной => lim_xŠ0 ^sinx/_x=1. т.к.ф-ция y=^sinx/_x и ф-ция y=cosx-чётные. sixx(-x)/-x=-sinx/-x=sinx/x,то доказанное нер-во (*) справедливо и при x<0. (см.рис.2). lim_xŠ∞^sinx/_x= lim_xŠ∞(sinx*¹/_x)=0. Примеры: 1) lim_xŠ0^tgx/_x=lim_xŠ0(^sinx/_x*¹/_cosx)=1*1=1; 2)lim_xŠ0 ^sinkx/_x= lim_xŠ0(^sin(kx)/_(kx)*k)=k*1=k; 3)lim_xŠ0^1-cosx/x²=[⁰/₀]=lim_xŠ0 2sin^{2 x}/₂/x²=lim_xŠ0 (sin^x/₂)/^x/₂*(sin^x/₂)/(^x/_2*2)=½.

№47. Второй замечательный предел и его следствия.

Рассмотрим переменную величину: (1+¹/_n)ⁿ;nÎN. Теорема 1: предел переменной величины (1+¹/_n)ⁿ заключён между числами 2 и 3 при nŠ∞, т.е. 2≤lim_nŠ∞(1+¹/_n)ⁿ ≤3. Док-во: по формуле Бинома-Ньютона имеем, что (1+¹/_n)ⁿ=С⁰_n*1ⁿ*(¹/_n)⁰+C¹_n*1^n-1*(¹/_n)¹+C²_n* 1^n-2*(¹/_n)²+C³_n*1^n-3*(¹/_n)³+…+Cⁿ_n*1⁰*(¹/_n)ⁿ =(≡) где С^m_n=^n!/_m!(n-m)!, где n!=1*2*3*…*n- это произвед-е первых n натуральных чисел. =(≡) =^n!/_0!n!*1+^n!/_1!(n-1)!*¹/_n+^n!/_2!(n-2)!*¹/n²+^n!/_3!(n-3)!*¹/n³+…+^n!/_n!0!*¹/nⁿ=1+1+^n(n-1)/_1*2*¹/n²+^{(n(n-1)(n-2))}/_1*2*3*¹/n³+…+¹/nⁿ= 1+1+¹/_1*2*(1-¹/_n)+¹/_1*2*3*(1-¹/_n)(1-²/_n)+^{(n(n-1)(n-2)*…*(n(n-1)))}/_1*2*3*…*n*¹/nⁿ= 1+1+¹/_1*2*(1-¹/_n)+¹/_1*2*3(1-¹/_n)(1-²/_n) +… +¹/_1*2*3*…*n*(1-¹/_n)(1-²/_n)*…*(1-^(n-1)/_n<1+1+¹/_1*2+¹/_1*2*3+…+¹/_1*2*3*…*n<1+1+¹/₂+¹/2²­+…+¹/2^n-1= S_n=(b1(1-qⁿ))/_1-q =1+(1-(¹/₂)ⁿ)/1-¹/₂=1+2(1-¹/2ⁿ)=3-¹/2^n-1<3, т.е. переменная величина {(1+¹/_n)ⁿ} ограничена сверху числом 3 кроме того очевидно, что эта переменная величина больше либо равна 2, из ____ видно, что 2≤(1+¹/_n)ⁿ<3, кроме того из ____=>,что переменная величина возрастает, т.к. все слагаемые положительные, а тогда наша переменная величина имеет предел, этот предел обозначают буквой “е”. ч.т.д. Опр: предел переменной величины {(1+¹/_n)ⁿ} называют число “е”,т.е. “е”=lim_nŠ∞(1+¹/_n)ⁿ. “е”-иррациональное, “е”=2,718281824. Теорема 2: ф-ция (1+¹/_x)^x при xŠ∞ имеет своим пределом число е, т.е. lim_хŠ∞(1+¹/_x)^x=е. Док-во: в теореме 1 мы установили, что lim_nŠ∞ (1+¹/_x)^x=е, если х-целое положительное число, докажем, что это верно если х дробное или отрицательное число. 1)пусть хŠ+∞, тогда для -х, n≤x<n+1, ¹/_n≥¹/_x>¹/_n+1, прибавим 1: 1+¹/_n≥1+¹/_x>1+¹/_n+1; (1+¹/_n)ⁿ⁺¹≥(1+¹/_x)^x>(1+¹/_n+1)ⁿ; найдём пределы переменных величин, стоящих в левой и правой частях нер-ва. lim_nŠ∞(1+¹/_n)ⁿ⁺¹= lim_nŠ∞(1+¹/_n)ⁿ *(1+¹/_n)=е*1=е. lim_nŠ∞(1+¹/_n+1)ⁿ=lim_nŠ∞^{((1+1/n+1)n+1)}/_(1+1/n+1)=^е/₁=е. след-но по теореме о пределе промежуточной переменной предел lim_nŠ+∞(1+¹/_x)^x=е. 2)хŠ-∞, введём новую переменную t по формуле t=-x-1=-(x+1)=>x=-t-1=-(t+1). Если хŠ-∞,то tŠ+∞, получаем: lim_хŠ-∞(1+¹/_x)^x= lim_хŠ+∞(1-¹/_t+1)^-t-1= lim_tŠ+∞(^t/_t+1)^-t-1= lim_tŠ+∞(^t/_t+1)^t+1= lim_tŠ+∞(1+¹/_t)^t+1= lim_tŠ+∞(1+¹/_t)^t * (1+¹/_t)=е*1=е, таким образом lim_хŠ∞(1+¹/_x)^x=е. – 2-ой замечательный предел(*). Замечание: пусть хŠ∞, то αŠ0=> равенство (*) я могу переписать в виде: lim_αŠ∞(1+α)^1/α =е. Примеры (см.на др.стороне.) Логарифмы с основанием е называются натуральными или неперовыми по имени одного из первых изобретателей логарифмических таблиц математика Непера (1550-1617). Если е^у=х, то у называют натуральным логарифмом числа х или у=lnx.

№48. Сравнение бесконечно малых.

Пусть lim_xŠaα(x)=0, lim_xŠaβ(x)=0. Найдём lim_xŠa^α(x)/_β(x)=[⁰/₀]. 1)опр.1. если предел отношения ^α(x)/_β(x) при xŠa равен С, где С=const отличное от нуля то α(x) и β(x) называются бесконечно малыми одного и того же порядка, т.е. lim_xŠa^α(x)/_β(x)=С, С=сonst, С=0; 2)опр.2. Если предел α(х), β(x) при xŠa=0, то α(х) называется бесконечно малой величиной более высокого порядка или β(x), т.е. lim_xŠa^α(x)/_β(x)=0; α(х)=0 (β(х)). α(х)–есть 0-мало от β(x). 3)опр.3. Если lim_xŠa^α(x)/_β(x)=1=>назыв. эквивалентными бесконечно малыми.=> α(х)~β(x). 4)опр.4. Если lim_xŠa^α(x)/[β(x)]^k=const, где С≠0, то α(х) называется бесконечно малой величиной порядка k относительно β(x). 5)Опр.5. Если lim_xŠa^α(x)/_β(x)-не сущ., то α(х) и β(x) называются несравнимыми б.м.в. Примеры№1: (см.на др.стороне).Теорема 1: Если α(х) и β(x) –эквивалентные б.м.в. при xŠa, то α–β – есть б.м.в. более высокого порядка чем α или β. lim_xŠa^α-β/_α=0; lim_xŠa^α-β/_β=0. Док-во: пусть α(х) эквивалентно β(x) при xŠa=> lim_xŠa^α(x)/_β(x)=1= ^β(x)/_α(x)=1. Рассм. lim_xŠa^α-β/_α= lim_xŠa(1-^β/_α)=1-lim_xŠa ^β/_α=1-1=0=> α–β=0(α). lim_xŠa ^α-β/_β= lim_xŠa(^α/_β-1)= lim_xŠa^α/_β -1=1-1=0=> α–β=0(β). Теорема 2,обратной 1. Если разность 2-х б.м.в. α(х)-β(x) при xŠa есть б.м.в. и относит. α(х) и β(x), то α и β – есть эквивалентные б.м.в.,т.е. α(х)-β(x)=0 (α(х))=>α(х)~β(x) и α(х)-β(x)=0 (β(х))=>α(х)~β(x). Док-во: т.к. α(х)-β(x)=0(α(х))=> lim_xŠa(^{α(х)-β(х)}/_α(х))=0=> lim_xŠa(1-^β/_α)=0=> lim_xŠa 1- lim_xŠa^β/_α=0 или lim_xŠa^β/_α=1=>α(х)~β(x). α(х)-β(x)=0 (β(х))= lim_xŠa ^α-β/_β=0=> lim_xŠa (^α/_β-1)=0=> lim_xŠa ^α/_β=1=> α(х)~β(x). (Примеры№2 см.надр.стороне).

Дата добавления: 2015-01-03