Сложность объекта моделирования

Сложность объекта моделирования. Субъективные и объективные аспекты сложности. Редукция сложности в задачах моделирования

Моделирование, наряду с теорией и экспериментом, является одной из фундаментальных методологий познавательно-созидательной деятельности. Оно особенно эффективно в тех случаях, когда возникает необходимость решения сложных, широкомасштабных, априорно неопределенных, некорректных и тому подобных задач.

Сложность – определяется мерой Хартли (кол-во информации об объекте) – полное число состояний объекта.

С помощью внешнего анализа рассматриваются общие свойства объекта и количество информации поступающей к эксперту (цель объекта {по целевой функции объект может быть одноцелевым и много целевым}, кол-во – размерность) по входу и выходу системы.

В результате оценивания внешней сложности возможны следующие варианты:

— если размерность не велика, то строится математическая модель

— если размерность велика, то необходимо произвести редукцию для снижения сложности

Внутренне содержание объекта – выделение частей, существенных для моделирования. Для структуризации существуют следующие методы:

- базовые (стратификация, декомпозиция)

- прикладные (использование стратификации и декомпозиции, но приоритет больше на какой-то)

Стратификация – определение уровней анализа (для моделирования) – используется принцип интроспективности – вычленение необходимых аспектов объекта, относящиеся к целям моделирования.

Декомпозиция – расчленяет на заданном уровне анализа (на выделенной страте) целостный объект моделирования на части (необходимо определить основание декомпозиции)

В результате использования этих методов возникает усложнение связанное с увеличением информации о системе пропорционально кол-ву компонент системы + возникают отношения между компонентами (принцип Парето).

Чем глубже анализ, тем больше информации, тем сложнее моделирование объекта, следовательно, необходимо определить:

1. уровни детализации;

2. задачи, с которыми работает;

3. точность, которая необходима с итоге.

Сложность бывает:

— структурная (характеристики: количественная {главная} – кол-во элементов и связей между ними; качественная - конфигурация {бывает последовательная, иерархическая}-это качественная сложность структуры).

— функциональная – выделение функции для каждого элемента, но морфологическая конфигурация подчиняется вложенности (включению) – морфологическое дерево. Функциональная сеть – запутанное дерево. Функциональная сложность (морфологический слой – обязательно учитывается) для построения функций.

Возможно, использование структурно-функциональной или функционально-структурной сложности (зависит от необходимого приоритета). Структурно-функциональная: структура не меняется, функции элемента могут меняться. Функционально-структурная: модели Фохта – функциональная основа постоянна, а структура меняется. [Функция-подфунция-до элементарной. Далее струится на этой основе структура снизу-вверх].

4. Концептуальная математическая метамодель объекта и её применение для решения задач моделирования

Математическое моделирование и модель

Математическое моделирование - это теоретико-экспериментальный метод познавательно-созидательной деятельности; это метод исследования и объяснения явлений, процессов и систем (объектов-оригиналов) на основе создания новых объектов - математических моделей.

Под математической моделью принято понимать совокупность соотношений (уравнений, неравенств, логических условий, операторов и т.п.), определяющих характеристики состояний объекта моделирования, а через них и выходные значения - реакции, в зависимости от параметров объекта-оригинала, входных воздействий, начальных и граничных условий, а также времени.

Математическая модель, как правило, учитывает лишь те свойства (атрибуты) объекта-оригинала, которые отражают, определяют и представляют интерес с точки зрения целей и задач конкретного исследования.

Анализ объекта показывает следующие свойства объекта:

— структура (морфологическое);

— функция (поведение);

— способ организации.

Как правило, рассматриваются динамические (активные) системы (живые). Организация системы – целевая (внутренняя или цель из вне) => механизм для достижения цели.

Функционирующие системы (живые, антропогенные - созданные человеком). Автомобиль – задание цели водителем.

Математическая метамодель – последовательность создания:

— морфология (структура)

— функции

— задачи (раскрытие функции)

— алгоритм (реализация функции через задачу)

— качество (значение функции в соответствии с целью)

Объект моделирование имеет следующие компоненты:

— строение

— поведение

— организация

Модель объекта:

— морфология (5 кортежей)

— функции (5 кортежей)

— целевое управление (5 кортежей)

— эпиморфные отношения компонентов

6. Метод блочных альтернативных сетей /БАС/ при решении задач моделирования

Этот метод организует данные и информацию. Он дает возможность группировать информацию по различным семантическим, ассоциативным или другим признакам. Дает возможность создания поименованных информационных массивов. Организовывать различные последовательности массивов в соответствии с требованиями решаемых задач. В рамках методологии блочных альтернативных сетей в отличие от морфологического ящика есть возможность избежать полного перебора элементов полного комбинирования за счет отсечения ненужных ветвей на каждом шаге прохождения сети. Это обеспечивает относительно быструю сходимость решений.

Архитектура блочной альтернативной сети (АБАС)

Основой АБАС является элементарный блок альтернатив (ЭБА). Пусть он характеризуется совокупностью атрибутов:

А_∑= {A_∑й: i=1, …, N_У} и

А_∑i= {б_јι: ј=1, …, m_У}.

Вводим понятие признака:

П_∑= {П_∑й: i=1, …, N_У} и

П_∑i= {р_јι: ј=1, …, m_У}.

А_∑ ∞ П_∑

А_∑i ∞ П_∑i

б_јι ∞ р_јι

Выбирая некий атрибут A_й для него можно представить следующую структуру:

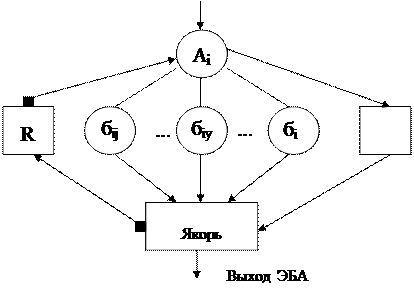Рис. 14.1. Первичное дерево иерархии

Развитие дерева с точки зрения ЭБА все сводится к добавлению замыкающей вершины (которая называется в нашем случае якорем).

б_јι – являются альтернативами α_јι+1 . Таким образом получается структура являющаяся структурной альтернативой. Использование такой структуры для автоматического выбора альтернатив требует ее расширения. Прежде всего, введем вершину обратной связи (R) – рекурсия, дает возможность организовывать циклы.

Если из совокупности атрибутов некоторые не используются, но представлены в виде блока возникает необходимость игнорировать или обходить такой блок. Для этого вводится еще одна вершина – транзитная (Т_i). Таким образом получаем законченную структуру ЭБА для некоторого блока. Данная структура является развернутой, она может быть свернута и представлена следующим образом:

Рис. 14.2. Свернутая структура ЭБА

Целесообразно использовать при формировании сетей. Представленные структурные схемы (рис. 14.1 и 14.2) дают возможность синтезировать различные архитектуры сетей, которые будем называть блочными альтернативными сетями (БАС) и обозначать N_a. В сетях вершины в свернутом виде представляют собой элементарные блоки и определяются, как супер - вершины. Формирование таких сетей осуществляется. В соответствии с существующей теорией синтеза структурных схем.

Варианты БАС:

1) последовательная сеть N_a

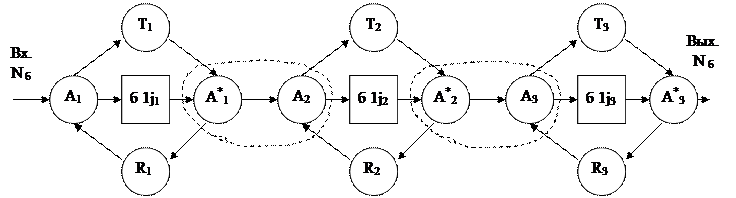
2) параллельная структура N_a

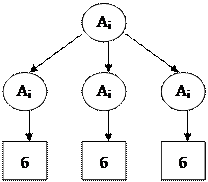
Для таких структур можно формировать параллельную структуру сети:

3) последовательно параллельные структуры N_a

Первые два (и более) блоков последовательные, а два (и более) параллельных блоков.

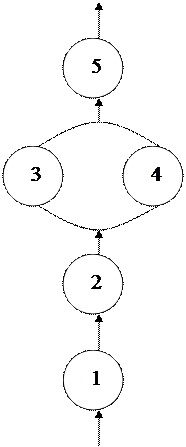
4) Параллельно последовательные структуры N_a

Работа посредством включения алгоритма навигации на сетях реализован четырьмя возможными методами: последовательная, параллельная и смешанные навигации. Рассмотрим навигацию элементарного блока альтернатив. Маршруты могут быть внутриблоковыми, межблоковые, сетевые.

Дата добавления: 2015-01-03