АЦП с преобразованием напряжения в частоту

В интегрирующих АЦП входное напряжение преобразуется в интервал времени, который измеряется путем заполнения тактовыми импульсами заданной частоты. Такие АЦП отличаются простотой и хорошим подавлением помех. Аналогичные характеристики могут быть получены при преобразовании напряжения в частоту импульсов с подсчетом последних на заданном интервале времени. По принципу действия и свойствам такой АЦП может быть отнесен к интегрирующим.

6. АЦП: основные параметры и характеристики.

Точность АЦП определяется рядом его характеристик, в том числе интегральной и дифференциальной нелинейностью, смещением нуля и погрешностью наклона характеристики преобразования, точностью источника опорного напряжения, температурными эффектами и характеристиками по переменному току.

Точность АЦП по постоянному току обычно выше, чем по переменному и лучше описывается его характеристиками – для определения качества работы АЦП на переменном токе используется масса нестандартных характеристик, определяемых нестандартными методами.

Существует два наиболее популярных метода определения общей погрешности системы: среднеквадратический и наихудшего случая. Среднеквадратическая оценка определяется как корень квадратный от суммы квадратов всех составляющих ошибки. Этот метод применим при некоррелированности отдельных составляющих погрешности.

В методе наихудшего случая общая погрешность определяется суммированием всех составляющих ошибки. Эта оценка гарантирует, что погрешность никогда не будет больше.

Дифференциальная нелинейность (DNL)

Хотя и не упомянутая среди ключевых параметров АЦП, дифференциальная погрешность является первой из характеристик, по которым производится их выбор. Дифференциальная нелинейность характеризует, насколько далеки друг от друга могут быть два соседних кода. Она измеряется по изменению входного напряжения, выраженному в LSB. Необходимо отметить, что INL является интегралом от DNL, поэтому она и не включена в перечень ключевых параметров АЦП. Признаком хорошего качества для АЦП является объявление отсутствия пропуска кодов.

Интегральная нелинейность (INL)

Поскольку INL является интегралом от DNL, хорошая INL гарантирует хорошую DNL. INL характеризует насколько далека реальная характеристика преобразования АЦП от идеальной.

Смещение нуля и погрешность наклона

Смещение нуля и погрешность наклона могут быть достаточно просто откалиброваны с помощью микроконтроллера или цифрового сигнального процессора. В биполярной системе смещение нуля сдвигает характеристику преобразования, но не уменьшает числа возможных кодов. Есть два метода устранения ошибки в биполярной системе. В первом характеристика преобразования смещается по оси х и оси у так, чтобы совместить отрицательный конец характеристики преобразования с расчетным значением. Второй метод реализуется итерационно. Сначала подается нулевое напряжение на вход АЦП и определяется смещение нуля в биполярной системе. Затем выполняется коррекция наклона характеристики.

Ошибка наклона характеристики определяется как ошибка полной шкалы минус смещение нуля

Ошибка полной шкалы измеряется в месте последнего изменения выходного кода на характеристике преобразования при ее сравнении с идеальной характеристикой преобразования АЦП. Ошибка наклона легко корректируется программно по линейной модели у=(m1/m2)x, где m1 – наклон идеальной характеристики, а m2 – наклон реальной измеренной характеристики

Другие источники погрешности

Шум Шум, который наблюдается при попадании входного сигнала в точку изменения кода на характеристике преобразования и приводит к мерцанию выходного кода, часто не специфицируется в справочных листах на АЦП. Даже АЦП с высоким разрешением (16 и более разрядов), где такой шум преобладает благодаря малому размеру дискрета, шум не специфицируется. Иногда размах шума может достигать нескольких дискретов. Для подавления шума необходимо взятие и усреднение ряда выборок входного сигнала.

Опорное напряжение

Одной из наибольших потенциальных причин возникновения погрешности в АЦП является источник опорного напряжения. Часто встроенные в микросхему АЦП источники опорного напряжения не специфицируются должным образом. Рассмотрим три основных механизма возникновения погрешности: температурный дрейф, шум и изменение напряжения при вариациях нагрузки.

Температурный дрейф

Температурный дрейф – наиболее часто указываемая в спецификациях характеристика. Для примера отметим, как температурный дрейф опорного напряжения отражается на характеристиках АЦП (Рис.1.7). У 12-разрядного АЦП для обеспечения точности в пределах расширенного индустриального диапазона температур (-40°C - +85°C) дрейф опорного напряжения не должен превышать 4 ppm/°C. К несчастью не существует АЦП со встроенными источниками опорного напряжения, обеспечивающими такую стабильность. Если сузить рабочий диапазон температур до 10°C, то допустимую нестабильность можно повысить до 25 ppm/°C, однако и это требование трудно выполнимо для встроенных источников опорного напряжения.

Шум опорного напряжения

Это второй важный аспект опорного напряжения. Численная величина шума выражается среднеквадратическим значением или размахом. Если источник опорного напряжения имеет 2,5 В с размахом шума 500 мкВ (или среднеквадратичным значением 83 мкВ), этот шум составляет 0,02% и снижает уровень точности до 12 разрядов еще до выполнения каких либо операций по аналого-цифровому преобразованию.

7. АЦП: квантование по уровню и дискретизация по времени.

На рис.2.1 приведены типовые формы сигналов при аналого-цифровом преобразовании. На рис.2.1а приведен аналоговый сигнал, который подвергается преобразованию – это напряжение, изменяющееся во времени. Чтобы числа были удобнее для восприятия, предположим, что напряжение изменяется от 0 до 4,095 В. Отметим, что на блок схеме устройство разбито на две части: устройство выборки/хранения S/H и аналого-цифровой преобразователь ADC. Такое разбиение на две части соответствует теоретической модели аналого-цифрового преобразования. Устройство выборки/хранения необходимо для поддержания уровня входного сигнала постоянным в течение времени преобразования. На рис.2.1b изображен сигнал на выходе устройства выборки/хранения, который изменяется только в определенные периодически повторяющиеся моменты времени, остальное время он остается неизменным. Таким образом, при выборке сигнала (sampling) независимая переменная (время) из непрерывной превращается в дискретную. Как показано на рис.2.1c, АЦП вырабатывает цифровой сигнал, в котором каждому плоскому участку на кривой рис. 2.1b соответствует целое число из диапазона 0 – 4095. При этом вносится некоторая ошибка, поскольку количество чисел в диапазоне ограничено, а уровни плоских участков могут быть любыми. Например, двум участкам 2.1b с уровнями 2,5600 В и 2,5602 В будет на рис.2.1c поставлено в соответствие число 2560. Другими словами, квантование (quantization) превращает зависимую переменную (напряжение) из непрерывной в дискретную.

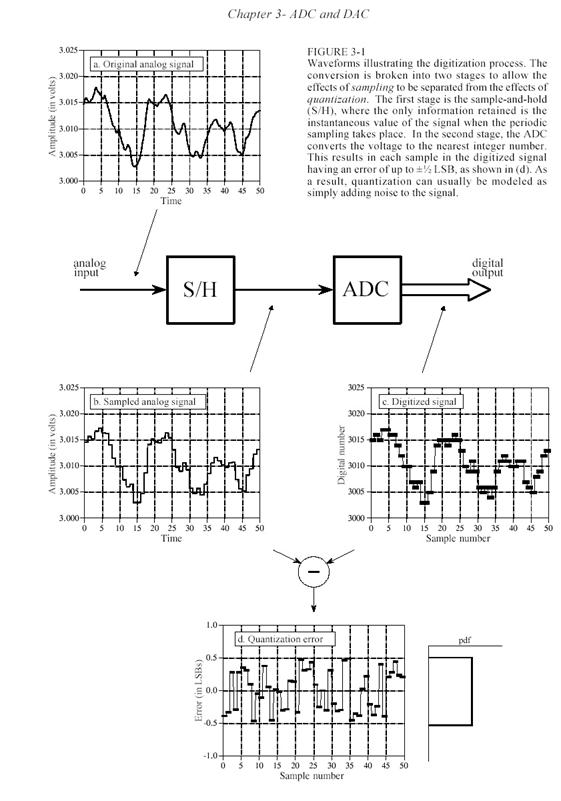
Рис.2.1

Мы намеренно не сравнивали рис. 2.1а срис.2.1с, поскольку здесь присутствуют оба эффекта. Раздельное рассмотрение целесообразно потому, что выборка и квантование вносят в сигнал различные искажения и управляются разными параметрами электроники. Кроме того, они не всегда используются вместе. Например, выборка без квантования используется в фильтрах на переключаемых конденсаторах.

Рассмотрим сначала влияние квантования. Любая из выборок в квантованном сигнале может иметь ошибку максимум на ±1/2 LSB (Least Significant Bit – термин для обозначения разности между соседними уровнями квантования). На рис.2.1d показана ошибка квантования для рассматриваемого примера, найденная путем вычитания кривой рис.2.1b из кривой рис.2.1c. Другими словами, цифровой сигнал рис.2.1c равен неквантованному сигналу рис.2.1b плюс ошибка квантования с рис.2.1d. Важно отметить, что ошибка квантования проявляется очень похоже на случайный шум.

Это определяет очень важную особенность ошибки квантования. Во многих случаях квантование не более, чем добавление определенного количества случайного шума к сигналу. Аддитивный шум равномерно распределен в пределах ±1/2 LSB, имеет нулевое среднее значение и стандартное отклонение 1/√12 LSB (0,29 LSB). Например, при прохождении сигнала через 8-разрядный квантователь к нему добавляется случайный шум с с.к.о. 0,29/256, т.е. примерно 1/900 от полной шкалы, 12-разрядный АЦП добавляет шум 0,29/4096≈1/14000, а 16-разрядный - 0,29/65536≈1/227000. Поскольку ошибка квантования является случайным шумом, число разрядов определяет случайную ошибку выходных данных.

Такое представление шума квантования очень плодотворно, поскольку случайный шум, генерируемый при квантовании, просто добавляется к шуму, уже содержащемуся в сигнале. Для примера представим входной сигнал с амплитудой 1,0 В содержит случайный шум со среднеквадратическим значением 1,0 мВ. 8-разрядное преобразование представляет 1,0 В числом 256, а 1,0 мВ составляет 0,255 LSB. Как известно, объединение случайных сигналов осуществляется путем сложения их дисперсий. Таким образом, общий шум цифрового сигнала будет равен √(0,255²+0,29²)=0,386 LSB. То есть, 8-разрядное преобразование увеличивает шум на 50%, но уже 12-разрядное преобразование практически ничего не добавляет к шуму и качество информации не ухудшается. При решении: сколько разрядов нужно в системе, ответьте на два вопроса: 1) Сколько шума уже содержится во входном сигнале? 2) Сколько шума можно допустить в выходном сигнале?

Когда такая модель шума неприемлема? Тогда, когда его нельзя считать случайным. Представим, что входной сигнал не изменяется на протяжении ряда последовательных выборок (См. рис. 2.2а) или даже изменяется в пределах ±1/2 LSB. При этом на выходе сигнал представляется одним и тем же числом, а ошибка квантования выглядит не как случайный шум, а как проявления некоторого порогового эффекта или странных искажений. Dithering является распространенным способом улучшения квантования таких медленноменяющихся сигналов. Как показано на рис.2.2 к сигналу добавляется небольшой случайный шум. В этом примере добавлен шум с с.к.о. 2/3 LSB и размахом примерно 3 LSB.

На рис. 2.2с показано, как добавления шума сказывается на выходном сигнале: даже при изменении входного сигнала в пределах ±1/2 LSB выходной случайным образом переключается между соседними состояниями.

Чтобы понять, как это улучшает качество преобразования, представим, что входной сигнал является постоянным напряжением 3,0001 В. Без зашумления взятие 10000 выборок даст нам 10000 одинаковых чисел 3000. После добавления шума выходные числа меняются, причем 90% из них будут равны 3000, а 10% - равны 3001. Усреднив выходной сигнал по по 10000 выборкам, получим результат близкий к 3000,1. Хотя одиночное преобразование имеет точность, ограниченную ±1/2 LSB, статистика может сделать его много лучше. На первый взгляд это парадоксальная ситуация: добавление шума обеспечивает больше информации.

Рис.2.2

Реализация зашумления может быть совершенно необычной. Можно, например, генерировать случайные числа на компьютере, затем, используя ЦАП, преобразовывать их в случайный шум и добавлять его к сигналу. После аналого-цифрового преобразования компьютер может вычесть эти случайные числа из выходной информации АЦП, используя арифметику с плавающей точкой. Этот элегантный способ, называемый subtractive dither, используется в сложных системах. Более простой способ заключается в использовании шума, уже имеющегося в сигнале.

Дата добавления: 2015-01-03