Часть 3

Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение.

C3

Решите систему уравнений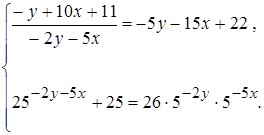

*C4

Дана правильная призма АВСА₁В₁С₁, где АА₁, ВВ₁ и СС₁ – боковые ребра. Сфера, центр которой лежит на ребре АА₁, пересекает ребро А₁С₁ в точке М и касается плоскости основания АВС и плоскости СВВ₁. Известно, что АВ = 12, А₁М: МС₁ = 3: 1. Найдите площадь боковой поверхности призмы.

C5

Известно, что уравнение 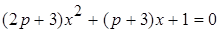имеет хотя бы один корень. Найдите все значения параметра 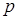, при которых число различных корней этого уравнения равно числу различных корней уравнения .

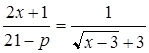~EndLATTest

Ответы к заданиям демонстрационного варианта по математике.

Ответы к заданиям с выбором ответа

№ задания	Ответ	№ задания	Ответ
А1		А6
А2		А7
А3		А8
А4		А9
А5		А10

Ответы к заданиям с кратким ответом

№ задания	Ответ
В1	– 0,25
В2
В3
В4
В5
В6
В7	4,5
B8
B9	20,2
В10
В11

Ответы к заданиям с развернутым ответом

№ задания	Ответ
С1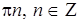
С2	– 2
С3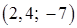
С4	324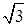
С5	– 1,5; – 1

Инструкция по оценке работ учащихся по математике

Первые 10 заданий А1–А10 – с выбором ответа из 4 предложенных вариантов, следующие 11 заданий В1–В11 – с кратким ответом в виде целого числа или числа, записанного в виде десятичной дроби.

Задание с выбором ответа (А1–А10) считается выполненным верно, если указан номер, которым обозначен верный ответ. Задание с кратким ответом (В1–В11) считается выполненным верно, если указано число, которое является верным ответом на данное задание. За верное выполнение заданий с выбором ответа и с кратким ответом выставляется 1 балл.

В работу включены 5 заданий с развернутым ответом С1 – С5, при выполнении которых требуется записать полное решение. Эти задания существенно различаются по уровню сложности. Два первых задания (С1 и С2) – повышенного уровня сложности, остальные три (С3 – С5) – высокого уровня сложности. Выполнение этих заданий оценивается экспертами. В зависимости от полноты и правильности ответа за выполнение заданий С1 и С2 выставляется от 0 до 2 баллов, за выполнение заданий С3 – С5 – от 0 до 4 баллов.

Критерии оценки выполнения заданий повышенного уровня (С1 и С2) отличаются от критериев оценки заданий высокого уровня сложности. Они не требуют от учащихся обосновывать приведенные ими решения. Это объясняется тем, что задачи С1 и С2 не являются совершенно новыми для учащихся, как это характерно для более сложных заданий С3 – С5. При решении задач С1 и С2 нужно, например, выделить несколько случаев, подлежащих рассмотрению (см. далее задание С1), или выбрать правильный порядок соответствующих преобразований и вычислений (см. задание С2). При этом в каждом из этих случаев надо применить стандартный способ решения, процедура которого достаточно отработана и, по-нашему мнению, не нуждается в приведении обоснований. Поэтому конкретизированные критерии оценки выполнения этих заданий фиксируют только правильность выделенных шагов решения, но не включают требования к их обоснованию.

Далее для каждой задачи С1 – С5 приводится один из возможных вариантов решения, который может быть представлен в работах учащихся, и даются рекомендации по оценке ответов учащихся, выбравших приведенный способ решения.

Подчеркнем, что приведенные записи решений не являются эталонами выполнения работы, которым обязаны следовать учащиеся.

ЗАДАНИЕ С1

Решите уравнение .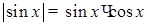

Решение:

1) Пусть 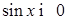, тогда 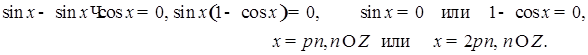Отсюда .

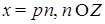2) Пусть , тогда 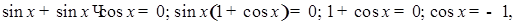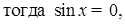что противоречит рассматриваемому случаю .

Ответ: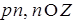

Баллы	Критерии оценки выполнения задания С1
	Приведена верная последовательность всех шагов решения: 1) рассмотрение случая 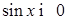и решение соответствующего уравнения, 2) рассмотрение случая и решение соответствующего уравнения. Все тождественные преобразования выполнены верно. Получен верный ответ.
	Приведена верная последовательность выделенных шагов решения. При решении одного из уравнений допущена одна описка или негрубая вычислительная ошибка, не влияющие на правильность дальнейшего хода решения. В результате этой описки или ошибки возможен неверный ответ.
	Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла.

ЗАДАНИЕ С2

Найдите нули функции .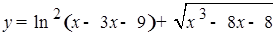

Решение:

1) Нули функции – это значения 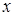, при которых 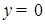. 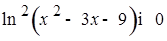и 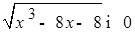, значит, их сумма равна 0, если каждое слагаемое обращается в нуль.

2)

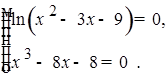
3) ; .

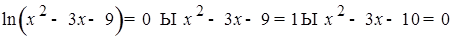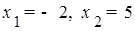4) Проверим, являются ли числа – 2 и 5 корнями второго уравнения системы:

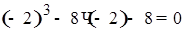, верное равенство, значит, – 2 – корень;

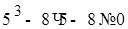, значит, 5 – не является корнем 2-го уравнения.

Ответ: – 2.

Дата добавления: 2015-01-03