
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замечания. 1) Проверку подстановкой при наличии ссылки на равносильность преобразований не следует считать недочетом
|
|
|
|
1) Проверку подстановкой при наличии ссылки на равносильность преобразований не следует считать недочетом.
2) Возможно решение и без введения новой переменной.
3) При решении квадратного уравнения запись дискриминанта и формулы корней квадратного уравнения не обязательна.
| Баллы | Критерии оценки выполнения задания С3 |
Приведена верная последовательность всех шагов решения:
1) сведение второго уравнения системы к квадратному уравнению относительно 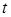 и его решение;
2) проверка «пригодности» корня и его решение;
2) проверка «пригодности» корня 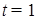 , выражение , выражение 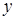 через через 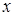 в случае в случае 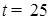 ;
3) решение системы, в котором приведены необходимые преобразования.
Обоснованы моменты решения: а) в п.2 имеется ссылка на знаменатель первого уравнения; б) в п.3 имеется ссылка на равносильность преобразований (словесная или с помощью знака ;
3) решение системы, в котором приведены необходимые преобразования.
Обоснованы моменты решения: а) в п.2 имеется ссылка на знаменатель первого уравнения; б) в п.3 имеется ссылка на равносильность преобразований (словесная или с помощью знака  ).
Все преобразования и вычисления верны. Получен верный ответ. ).
Все преобразования и вычисления верны. Получен верный ответ.
| |
| Приведена верная последовательность всех шагов решения. Обоснован ключевой момент а). Допустима описка, в результате которой может быть получен неверный ответ (например, в записи самого ответа пропущен минус). | |
Приведена верная последовательность всех шагов решения.
При этом получено и верно решено уравнение 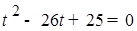 , значение , значение 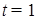 исключено.
Обоснован ключевой момент а).
Допустимы 1 – 2 негрубые ошибки или описки в вычислениях в шаге 3, не влияющие на правильность дальнейшего хода решения.
В результате этих ошибок может быть получен неверный ответ. исключено.
Обоснован ключевой момент а).
Допустимы 1 – 2 негрубые ошибки или описки в вычислениях в шаге 3, не влияющие на правильность дальнейшего хода решения.
В результате этих ошибок может быть получен неверный ответ.
| |
Общая идея, ход решения верны, но решение, возможно, не завершено: получено и верно решено уравнение 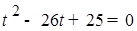 . Допускается, что значение . Допускается, что значение 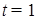 не исключено, а в случае t =25 составлена правильная система уравнений, но ее решение не завершено.
Обоснования ключевых моментов отсутствуют.
Допустимы негрубые ошибки в вычислениях или преобразованиях. В результате этих ошибок может быть получен неверный ответ. не исключено, а в случае t =25 составлена правильная система уравнений, но ее решение не завершено.
Обоснования ключевых моментов отсутствуют.
Допустимы негрубые ошибки в вычислениях или преобразованиях. В результате этих ошибок может быть получен неверный ответ.
| |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3, 4 балла. |
ЗАДАНИЕ С4
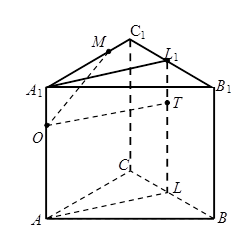
Дана правильная призма АВСА1В1С1, где АА1, ВВ1 и СС1 – боковые ребра. Сфера, центр которой лежит на ребре АА1, пересекает ребро А1С1 в точке М и касается плоскости основания АВС и плоскости СВВ1. Известно, что АВ = 12, А1М: МС1 = 3: 1. Найдите площадь боковой поверхности призмы.
 Решение:
Решение:
1) Так как призма правильная, то прямая АА1^АВС. По условию центр О сферы лежит на ребре АА1 и поэтому, по свойству плоскости, касательной к сфере, сфера с центром в точке О касается плоскости АВС в точке А. Значит, 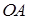 – радиус сферы.
– радиус сферы.
2) Пусть L и L 1 – середины ребер ВС и В 1 С 1 соответственно. Так как треугольник АВС – правильный, то 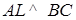 . А так как
. А так как 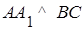 , то
, то 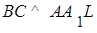 , т.е. плоскости СВВ1 и АLL 1 перпендикулярны. Пусть Т – точка касания сферы с плоскостью СВВ 1. Тогда ОТ – радиус сферы,
, т.е. плоскости СВВ1 и АLL 1 перпендикулярны. Пусть Т – точка касания сферы с плоскостью СВВ 1. Тогда ОТ – радиус сферы, 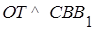 , значит, ОТ лежит в плоскости АLL 1. Тогда
, значит, ОТ лежит в плоскости АLL 1. Тогда 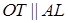 , а так как
, а так как 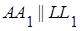 , то
, то 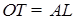 . Отсюда
. Отсюда 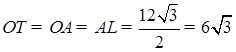 как высота правильного треугольника, со стороной 12.
как высота правильного треугольника, со стороной 12.
3) Точка М лежит на сфере. Поэтому  . По условию
. По условию 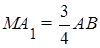 . Тогда
. Тогда 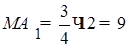 . Из прямоугольного треугольника ОМА 1 находим
. Из прямоугольного треугольника ОМА 1 находим 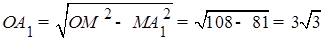 . Отсюда находим высоту призмы:
. Отсюда находим высоту призмы: 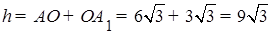 .
.
4) Площадь S боковой поверхности призмы найдем по формуле 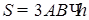 . Отсюда
. Отсюда 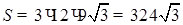 .
.
Ответ: 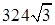 .
.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 341; Нарушение авторских прав?; Мы поможем в написании вашей работы!