Замечание. Решение, оцениваемое 2 баллами

Решение, оцениваемое 2 баллами

Решение, оцениваемое 3 баллами

1) А – точка касания сферы с плоскостью авс, – радиус сферы.

2) Пусть 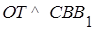. Тогда ОТ – радиус сферы, и .

3) . . Отсюда высота призмы .

4) Площадь S боковой поверхности призмы найдем по формуле 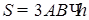. Отсюда .

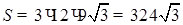1) Точка О – центр, а Т– точка касания сферы с СВВ₁ и

2) OT = OA = AL =

3) ; ^*

.

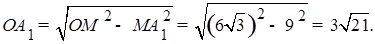4) Площадь S боковой поверхности призмы найдем по формуле 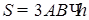. Отсюда

* Допущена негрубая ошибка в вычислениях.

Считается недочетом, если точные значения искомых величин заменены приближенными, например, записано, что OT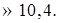

Баллы	Критерии оценки выполнения задания C4
	Приведена верная последовательность всех шагов решения: 1) установлено положение точки касания сферы с плоскостью основания; 2) установлено положение точки касания сферы с боковой гранью; 3) найдено соотношение между ребром основания призмы и радиусом сферы; 4) найдена высота призмы; 5) вычислена площадь боковой поверхности призмы. Использованы верные формулы при нахождении искомых величин. Верно обоснованы все ключевые моменты решения: а) положение точки касания сферы с плоскостью основания; б) положение точки касания с боковой гранью. Проведены верные вычисления. Получен верный ответ.
	Имеются все шаги 1) – 4) решения. Использованы верные формулы. Приведены утверждения, составляющие ключевые моменты а), б) решения. Допустимо отсутствие обоснований ключевых моментов решения или неточности в обоснованиях1, но не грубые ошибки. Допустима описка и/или негрубая ошибка в вычислениях, не влияющие на правильность хода решения. В результате этой описки и/или ошибки возможен неверный ответ.
	Имеются шаги 2) – 4) решения. Использованы верные формулы. Утверждения, составляющие ключевые моменты а) и б) решения, либо оба отсутствуют, либо приведено только одно из них. Но сами ключевые моменты использованы в решении. Приведенные в решении обоснования не содержат грубых ошибок. Допустима описка и/или негрубая ошибка в вычислениях или рассуждениях, не влияющие на правильность хода решения. В результате этой описки и/или ошибки возможен неверный ответ.
	Ход решения правильный, но решение не завершено. Верно найдено соотношение между радиусом сферы и ребром основания призмы, то есть в вычислениях и рассуждениях верно использовано положение центра сферы. Допустимо отсутствие обоснований или неточности в обоснованиях. Приведенные в решении обоснования не содержат грубых ошибок. Допустимы негрубые ошибки в вычислениях или рассуждениях, не влияющие на правильность хода решения.
	Все случаи решения, которые не соответствуют выше указанным критериям выставления оценок 1 – 4 баллов.

ЗАДАНИЕ С5

Известно, что уравнение имеет хотя бы один корень. Найдите все значения параметра 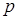, при которых число различных корней этого уравнения равно числу различных корней уравнения .

Решение:

1) Если 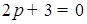, , 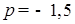то первое уравнение – линейное: . У него один корень .

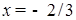2) Если 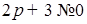, то первое уравнение – квадратное. Найдем его дискриминант:

. Если , то .

Значит, уравнение имеет корни только при 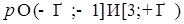. Причем, пр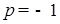и и 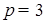– корень один, а при – два корня.

3) Пусть . Тогда при 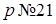второе уравнение примет вид

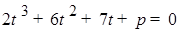, . Исследуем функцию 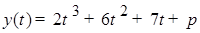. Найдем производную .

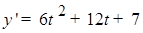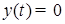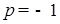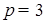4) Так как , то возрастает на всей числовой прямой . Поэтому уравнение или не имеет корней, или имеет только один корень. Первый случай невозможен по условию задачи. Значит, (см. 1) и 2)) или , или , или .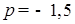

5) Если 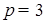, то получаем уравнение . По условию 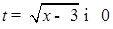, и так как возрастает, то . Значит, неотрицательных корней у уравнения нет.

Если 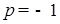, то получаем уравнение . Так как 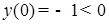, и функция 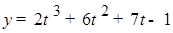непрерывна, то уравнение имеет корень на промежутке .

Если 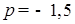, то получаем уравнение . Так как , то так же, как и в случае 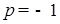, уравнение имеет корень на промежутке .

Ответ: ; .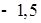

Дата добавления: 2015-01-03