Элементы комбинаторики

ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ

The Middle East crisis and the USA foreign policy

Пример оформления статьи на английском или немецком языке

Pankova Anna Nikolaevna, Moscow State University,

postgraduate student, the Faculty of Political Science

E-mail: [email protected]

[Информация о соавторах, если есть]

Text. Text. Text. Text. Text[3]. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text[4]. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text. Text.

References:

1. Fromkin D. A Peace To End All Peace. New York, 1989.
2. Held C. Middle East Patterns: Places, Peoples, and Politics. London, 2000.

[1] Ссылка на источник.

[2] Ссылка на источник.

[3] Ссылка на источник.

[4] Ссылка на источник.

К основным понятиям комбинаторики относятся размещения, перестановки, сочетания.

Определение. Размещениями из n элементов по m называют такие их соединения, которые отличаются друг от друга самими элементами или их порядком.

Число всех размещений из n элементов по m считается по формуле:

.

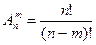Определение. Перестановками из n элементов называются их соединения, отличающиеся друг от друга только порядком входящих в них элементов.

Число всех перестановок из n различных элементов равно:

.

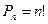Определение. Сочетаниями из n элементов по m называются их соединения, различающиеся друг от друга только самими элементами.

Число сочетаний из n различных элементов по m считается по формуле:

.

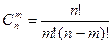Также имеются простые формулы:

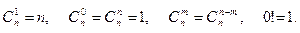
Задача. Сколькими различными способами собрание из 40 человек может выбрать из своей среды председателя собрания и секретаря?

Решение. Число различных способов равно числу всевозможных размещений из 40 по 2: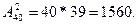

Задача. Сколько пятизначных чисел можно записать при помощи цифр 1,2,3,4,5, если каждая цифра входит в изображение числа только один раз?

Решение. Число пятизначных чисел, которое можно написать при помощи цифр 1,2,3,4,5, равно числу всевозможных перестановок из пяти элементов: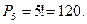

Задача. В коллективе из 20 человек следует выбрать 3 ораторов. Сколькими способами это можно сделать?

Решение. Число различных способов равно числу всевозможных сочетаний из 20 по 3: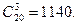

Имеется 100 одинаковых по внешнему виду деталей, среди которых 97 стандартных, а остальные бракованные. Берется наудачу одна деталь. Очевидно, что события А и В, состоящие соответственно в том, что деталь окажется стандартной и бракованной, не равновозможные, событие А более возможно, более вероятно, чем В.

Определение. Число, являющееся выражением меры объектив­ной возможности наступления события, называется его вероятностью.

Вероятность события А будем обозначать символом Р(А) (от слова probabilities — вероятность). Читается: вероятность события А.

Определение. Вероятность события А равна отношению числа случаев т, благоприятствующих ему, из общего числа п единственно возможных, равновозможных и несовместимых случаев, к числу п, т. е.

Р (А) = т/п.

Таким образом, для нахождения вероятности события необходи­мо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместимых случаев, подсчитать общее число их п и число случаев т, благоприятствующих данному событию, и затем произвести расчет по указанной формуле.

Пример. В условиях сформулированного примера найти вероятность того, что взятая наудачу деталь окажется стан­дартной.

Решение. Представим мысленно, что все детали занумерованы. Тогда должно быть ясно, что при взятии одной детали возможны 100 различных собы­тий (случаев), которые, как нетрудно видеть, являются единственно возможны­ми, равновозможными и несовместимыми. Появление любой из 97 стандартных деталей будет означать осуществление события А, или, как принято говорить, событию А благоприятствуют 97 из общего числа 100 случаев. Следовательно, вероятность события А равна:

Р (А) = 97/100 = 0,97.

Рассмотрим теоремы о свойствах вероятности события, вытекаю­щие из ее определения.

Теорема. Вероятность любого события не может быть от­рицательной и больше единицы.

Доказательство. Число случаев т, благоприятствующих любому событию, не может быть отрицательным и большим, чем общее число их п, т. е. 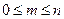. Деление неравенств почленно на п дает 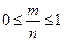, или приняв во внимание равенство 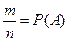, получим: , что и требовалось доказать.

Теорема. Вероятность достоверного события равна единице.

Доказательство. Свойство очевидно, так как достовер­ному событию должны благоприятствовать все п единственно воз­можных, равновозможных и несовместимых случаев, т. е. т = п.

Теорема. Вероятность невозможного события равна нулю.

Доказательство. Невозможному событию не может бла­гоприятствовать ни один из п единственно возможных, равновозможных и несовместимых случаев, т. е. т = 0. Отсюда следует сформули­рованное свойство.

Необходимо четко различать понятия вероятности и частости со­бытия. Вероятность события вычисляется до опытов и численно вы­ражает меру объективной возможности наступления события, а час­тость его определяется лишь после того, как результаты опыта стано­вятся известными.

Пример. Монета подброшена пять раз. Герб выпал два раза. Какова вероятность и частость выпадения герба?

Решение. Вероятность выпадения герба равна 1/2 = 0,5 (из двух воз­можных исходов при подбрасывании монеты выпадению герба благоприятствует один), а частость выпадения герба равна 2/5= 0,4 (событие наступило два раза в пяти испытаниях).

Задача. Подбрасывают две игральные кости. Найти вероятность собы­тия В, состоящего в том, что на них в сумме будет 10 очков.

Ответ: 3/36=1/12=0,083.

Задача. На каждой из 6 одинаковых карточек написаны по одной букве: А,Г,Н,О,Р,Ы. Какова вероятность того, что вынимая по одной четыре карточки, получим слово «горы»?

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь четыре карточки из шести, т.е. равно 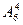- числу размещений из 6 элементов по 4. Благоприятствует появлению слова «горы» только один исход. Следовательно,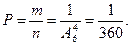

Задача. В бассейне содержится 7 лещей и 12 карпов. Какова вероятность того, что среди пяти пойманных рыб две окажутся лещами?

Решение. Всевозможных исходов может быть столько, сколько можно составить сочетаний из 19 рыб по 5, т.е. 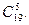При подсчете благоприятных исходов надо учесть, что каждая пара лещей может сочетаться с каждой тройкой карпов. Пар лещей может быть столько, сколько можно составить сочетаний из 7 элементов по 2, а троек карпов столько, сколько можно составить сочетаний из 12 элементов по 3. Тогда: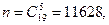 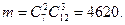Тогда искомая вероятность равна: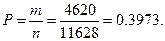

Задача. В партии из N изделий M бракованных. Их партии выбирается наугад n изделий. Определить вероятность того, что среди этих n изделий будет ровно m бракованных.

Решение: Общее число случае, очевидно, равно n= 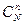, число благоприятных случаев: m= 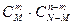. Отсюда вероятность интересующего нас события:

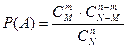
Задача. Среди 50 деталей три нестандартные. Взяты наудачу две дета­ли. Найти вероятность того, что они нестандартные.

Решение. Вероятность рассматриваемого события зависит от того, как производится отбор деталей.

Первый способ. Установив качество наудачу взятой детали, ее возвращают обратно, а после тщательного перемешивания берут следующую. При таком спо­собе отбора общее число различных исходов испытания равно 50 • 50 = 2500 (первой может оказаться любая из 50 деталей и она может сочетаться с любой из тех же 50 деталей при отборе второй детали), которые и являются единственно возможными, равновозможными и несовместимыми. Из них событию А, состояще­му в том, что обе детали будут нестандартными, благоприятствуют 3 • 3 = 9 ис­ходов (при отборе первой детали нестандартная может появиться в трех случаях, и каждый этот случай может сочетаться с тремя возможностями отбора нестан­дартной детали, когда будут брать вторую деталь). Следовательно, вероятность Р (А) = 9/2500 = 0,0036.

Второй способ. Взятая наудачу деталь обратно не возвращается. При таком способе отбора число различных исходов испытания равно 50 • 49 = 2450 (любая из 50 деталей, которая будет взята первой, может сочетаться с любой из остальных 49 деталей при отборе второй), которые и являются единственно воз­можными, равновозможными и несовместимыми. Из них событию В, заключаю­щемуся в том, что обе детали окажутся нестандартными, благоприятствуют толь­ко 3 • 2 = 6 случаев. Поэтому вероятность его Р (В) = 6/2450 = 0,0024.

Последний пример наглядно показывает, что вероятность события становится определенной лишь после того, как установлены условия испытания.

Задача. Игральная кость бросается один раз. Найти вероятности событий: A={четное число очков}, B={не менее 5 очков}, C={не более 5 очков}.

Ответ: P(A)=1/2, P(B)=1/3, P(C)=5/6.

Задача. В ящике из 15 шаров 4 белых. Наудачу вынимается шар, какова вероятность, что он черный.

Ответ: P(A)=11/15.

Задача. Игральная кость бросается один раз. Найти вероятности событий: A={четное число очков}, B={не менее 5 очков}, C={не более 5 очков}.

Ответ: P(A)=1/2, P(B)=1/3, P(C)=5/6.

Задача. В урне а белых и b черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение: Обозначим В – событие, состоящее в появлении двух белых шаров. Подсчитаем общее число возможных случаев n и число m, благоприятных событию В: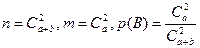

Приведенное выше определение вероятности события получило на­звание классического. Оно дает возможность рассматривать лишь собы­тия, которые распадаются на конечное число равновероятных случа­ев. Этот недостаток классического определения вероятности. Было построено понятие вероятности для случаев с бесконечным множеством исходов испытания. В общем виде задачу, которая привела к расширению понятия вероятности и к другому определению ее, можно сформулировать следующим об­разом.

На плоскости имеется область Gи область g в ней.

Площа­ди их равны S_G и S_g соответственно. В область Gбросается наудачу точка. Вероятность р того, что точка окажется в области g, принима­ется равной

p=G/g.

При этом предполагается, что точка может попасть в любую часть области G, а вероятность попадания в область gпропорциональна лишь ее площади и не зависит ни от расположения, ни от ее формы. Такое определение вероятности получило название геометрического.

Задача. Круглый диск радиуса Rразбит на два сектора. Длина дуги одного из них (заштрихованного) равна радиусу R.

По быстро вращаю­щемуся диску произведен выстрел. Найти вероятность попадания в этот сектор.

Решение. Площадь заштрихованного сектора S_g=R*R/2, а площадь круга S_G= 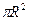. Согласно формуле геометрической вероятности вероятность искомого со­бытия р =0,5 .

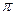Дата добавления: 2015-01-03