Теорема умножения вероятностей

Определение. Вероятность события А, найденная в предпо­ложении, что событие В наступило, называется условной вероятностью события А относительно события В.

Обозначать ее будем символом Р_В(А). В таком случае Р_В(А) означает вероятность события А, вычисленную в предположении, что событие В не наступило.

Пример. С первого станка на сборку поступило 200 деталей, из которых 180 годных, со второго — 300, из которых 260 годных. Найти вероятность собы­тия А, состоящего в том, что взятая наудачу деталь будет годной, и условные ве­роятности его относительно событий В и 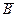, если событие В состоит в том, что эта деталь изготовлена на первом станке.

Решение. Вероятность события А равна отношению числа всех годных к общему числу изготовленных на обоих станках деталей: Р (А) =(180+260)/(200+300)=0.88. Условная вероятность события А относительно события В (вероятность того, что взятая наудачу деталь годная, если известно, что она изготовлена на первом станке) Р_В(А) = 180/200 = 0,9. Условная вероятность события А от­носительно события В, т. е. вероятность того, что взятая деталь годная, если из­вестно, что она изготовлена не на первом (на втором) станке, =260/300=0.87.

Теорема (умножения вероятностей). Вероят­ность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого относительно взятого первым, т. е.

Р (АВ) = Р (А) • Р_А (В) или Р (AB)= Р (В) • Р_В (А).

Задача. Среди 25 электрических лампочек четыре нестандартные. Найти вероятность того, что две взятые одновременно лампочки окажутся не­стандартными.

Решение. Искомое событие состоит в том, что нестандартными будут и первая (событие А) и вторая (событие В) лампочки. Но Р(А) = 4/25, а Р_А (В) = 3/24, так как при наступлении собы­тия А общее число лампочек и число нестандартных среди них по сравнению с первоначальным уменьшится на одну. Таким образом, Р (АВ) = 4/25*3/24=0,02.

Задача. На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны.

Решение. Событие А – первый взятый наугад заказ, В – соответственно второй, P (АВ) = 5/8*4/7=20/56.

Определение. Событие А будем называется зависимым от события В, если вероят­ность события А меняется при наступлении события В. Совершенно естественно называть событие А независимым от события В, если ве­роятность события А не изменяется при наступлении события В. Сле­довательно, если событие А независимо от события В, то

.

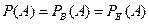Однако независимость и зависимость со­бытий обладают свойством взаимности, а именно справедлива теорема:

Теорема. Если событие А независимо от события В, то и В не­зависимо от А. Если же событие А зависимо от события В, то и собы­тие В зависимо от А.

Определение. События А и В называются независимыми, ес­ли вероятность одного из них не изменяется при наступлении другого. В противном случае события А и В называются зависимыми.

Независимость более чем двух событий может быть различной.

Определение. События А, В, С,...., К называются попар­но независимыми, если независимы между собой любые два из них.

Определение. События А, В, С,..., К называются независимыми в совокупности, если вероятность каждого из них не меняется при наступлении других событий (одного или нескольких в любой комбинации и в любом числе).

Независимость событий в совокупности является более сильным требованием, чем их попарная независимость.

Теорема умножения вероятностей для двух независимых событий имеет более простой вид.

Теорема. Вероятность произведения двух независимых событий равна произведению их вероятностей:

Задача. Считая вероятность безотказной работы станка в течение смены равной 0,9, найти вероятность безотказной работы двух станков в течение смены.

Решение. Считая события А и В, состоящие в безотказной работе в те­чение смены соответственно первого и второго станков, независимыми и применяя к ним теорему умножения вероятностей получим: Р (АВ) = 0,9 • 0,9 =*0,81.

Теорему умножения вероятностей легко обобщить на любое конеч­ное число событий.

Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произве­дения предшествующих каждому из них событий, т. е.

Р (АВС...КL) = Р(А) • Р_А (В) • P_AB (С)...P_ABC…K (L).

Если события А, В, С,..., K, L независимые в совокупности, то фор­мула упрощается, а именно:

Р (АВС...КL) = Р(А) • Р (В) • P (С)... P (L).

т. е. вероятность произведения конечного числа независимых в со­вокупности событий равна произведению их вероятностей.

Задача. На десяти карточках напечатаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Найти вероятность того, что три наудачу взятые и поставленные в ряд карточки составят число 125.

Решение. Искомое событие О произойдет, если первой будет взята карточка с цифрой 1 (событие А), вторая — с цифрой 2 (событие В), третья — с цифрой 5 (событие С). Вероятность его по теореме умножения вероятностей для трех. зависимых событий: P= 1/10*1/9*1/8=1/720=0,0014.

Задача. Рабочий обслуживает четыре однотипных станка. Вероят­ность того, что станок (любой) в течение часа потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станках независимые, найти вероятность того, что в течение часа потребуют внимания рабочего: а) все четыре станка; б) ни один станок; в) по крайней мере один станок.

Решение. а) Обозначим через А₁, А₂, А₃, А₄ события, состоящие в том, что в течение часа потребуют внимания рабочего соответственно первый, второй, третий, четвертый станки. По теореме умножения вероятностей для независимых событий вероятность того, что в течение часа все станки потребуют внимания ра­бочего, т. е. произойдут события все эти события, равна: P= 0,6⁴ = 0,1296.

б) Вероятность того, что в течение часа станок (любой) не потребует внимания рабочего по правилу нахождения вероятности противоположного события: Поэтому вероятность события В, заключающегося в том, что в течение часа ни один станок не потребует внимания рабочего, т. е. произойдут события : P(В)= 0,4⁴ = 0,0256.

в) Событие, состоящее в том, что в течение часа по крайней мере один из четырех станков потребует внимания рабочего, и событие В, рассмотренное в пункте «б», противоположные. Поэтому вероятность искомого события 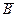: 1- 0,0256 = 0,9744.

Задача. Студент выучил 20 вопросов из 25. Какова вероятность, что он ответит на три предложенных ему вопроса, ответит хотя бы на 1 вопрос?

Решение: A-студент ответит на первый вопрос, В - студент ответит на второй вопрос, С - студент ответит на третий вопрос, тогда: P(студент ответит на все три вопроса) = . Т.е. P=20/25*19/24*18/23=57/115=0.5. D – студент ответит хотя бы на один вопрос. Противоположное событие – что не ответит ни на один вопрос. P(D) = 1-5/25*4/24*3/23=0.996.

5. Призма (от др.-греч. πρίσμα (лат. prisma) «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.

Призма является разновидностью цилиндра (в общем смысле).

Дата добавления: 2015-01-03