Доказательство. Достаточный признак возрастания (убывания) функции

Теорема 2.

Достаточный признак возрастания (убывания) функции.

Замечание.

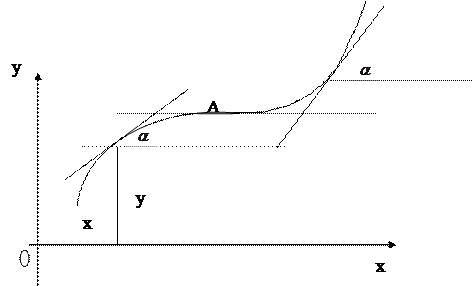Геометрически утверждение теоремы сводится к тому, что для графика возрастающей дифференцируемой функции касательные образуют с положительным направлением оси Ох острые углы (tg = (x)) или в некоторых точках А параллельны оси Ох. Для графика убывающей дифференцируемой функции все касательные образуют тупые углы с положительным направлением оси Ох или параллельны ей.

у=f(x)

1. Если производная дифференцируемой функции положительна внутри некоторого промежутка, то функция возрастает на этом промежутке.

2. Если производная дифференцируемой функции отрицательна внутри некоторого промежутка, то функция убывает на этом промежутке.

1.Пусть, например, дифференцируемая функция f (x) такова,

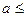
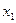
что f^/(x)>0 при a<x<b. Для любых двух значений 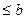,принадлежащих промежутку (a, b), в силу теоремы о конечном приращении функции имеем f(x₂) – f(x₁)=(x₂-x₁) f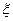^/(), где 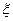-промежуточное значение между x₁ и x₂ и, следовательно, лежащее внутри промежутка (a,b). Так как x₂-x₁>0 и f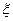^/()>0,то отсюда получим f(x₂)- f(x₁)>0 или f(x₂)> f(x₁).

Следовательно, функция f(x) возрастает на промежутке (a,b)

2. Доказательство второй части этой теоремы совершенно аналогично доказательству первой части её.

Функция возрастающая (или убывающая), называется монотонной.

Промежутки, в которых данная функция возрастает или убывает, называется промежутками монотонности этой функции.

Пример:

Исследовать на возрастание и убывание функцию: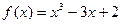

Решение:

Находим производную: . Производная обращается в нуль при значениях: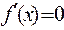

Эти значения разбивают всю бесконечную ось Ох на три промежутка: ;-1], [-1;1], [1;+ ), внутри каждого из которых производная f^/(х) сохраняет постоянный знак.

Следовательно, функция f(x) возрастает на ;-1) (1;+ ],

убывает на (-1;1).

Дата добавления: 2015-01-03