Доказательство. Теорема 2 (второе правило)

Теорема 2 (второе правило).

Если для дифференцируемой функции f(x) в некоторой точке х₀ ее первая производная f'(x) равна нулю, а вторая производная f''(x) существует и отлично от нуля, т. е. f'(x₀)= 0, f''(x₀)≠0, то в этой точке функция f(x) имеет экстремум;

а именно:

1) если f''(x₀)>0, то f(x₀)- минимум функции f(x), и

2) если f''(x₀)<0, то f(x₀)- максимум функции f(x).

1. Положим, что f'(x₀)=0, f''(x₀), пусть x=x₀+ 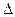x₀ - точка близкая к x₀.

Т.к. вторая производная f''(x) есть производная от первой производной f'(x), то имеем:

Таким образом, переменная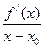

стремится к пределу f^//(x₀)≠0, а значит, начиная с некоторого момента, это величина имеет знак своего предела в нашем случае плюс. поэтому:

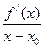>0 при 0<|x-x₀|<E, где Е - достаточно малое положительное число.

Отсюда получаем, что числитель и знаменатель этой дроби имеют одинаковые знаки и, следовательно, f^/(x₀)<0 при х₀-Е<x<x₀ и, следовательно, f^/(x₀)>0 при х₀<x<x₀+Е.

Мы видим, что производная f^/(x) при переходе через точку х₀ меняет свой знак с минуса на плюс, т.е. минимум функции.

3) Аналогично доказываем, что если f^/(x₀)=0 и f^//(x₀)<0, то

f(x₀)- минимум функции f(х).

Задача.

Дан треугольник АBC, основание которого AC=b и высота BL=h. Найти прямоугольник наибольшей площади, который можно вписать в этот треугольник.

B

Решение.

	K

D E

		C
		x
	A

Обозначим высоту KL прямоугольника через х, основание DE через у. Тогда площадь его S=xy. Переменные х и y не являются независимыми, они связаны некоторыми соотношением.

В самом деле из подобия треугольников DBE и ABC, учитывая, что высоты их BK и BL пропорциональны основаниям DE и AC имеем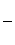

или т.к. BK=h-x, DE = y, BL=h, AC=b,

то у=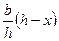

исключая у из выражения для S находим

S =

Ищем максимум для этой функции

S =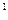

S 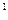=0 h-2x=0 x=

Легко видеть, что значение х действительно даст максимум функции S. В самом деле, составляя вторую производную, будем иметь

следовательно, при площадь S имеет максимум, причем из формулы S= 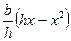получаем S_max=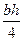

Ответ: площадь наибольшего прямоугольника, вписанного в треугольник, равна половине площади этого треугольника.

Дата добавления: 2015-01-03