Если каждая сторона будет равна , то площадь будет наименьшей

Задача № 5.

На изготовление ящика с крышкой расходуется 108 дм ² фанеры. Стороны основания относятся как 1: 2. Найдите линейные размеры ящика, при которых его объем наибольший.

Решение: S_ПОЛН. = 2ab + 2ac +2bc=2(ab+ac+bc)=108

аb+ac+bc=54

аb-54= - ac-bc

54-ab=с(а+b)

а с=

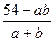
с

b

Пусть а=х, x 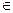(0;+ ), тогда b=2x, c=

V=a b c= x 2x = 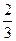x (54-2 ) = x (27- )

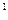
) ) ) - x 2x =

=36- 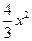- =36-4x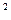

V^/ (x)=0 36-4x 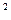=0

36=4x²

=9

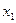=3

=-3

a=3дм, b=6дм, с=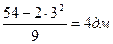

Ответ: 3дм, 6дм, 4дм.

Задача №6. Найти наибольший объем цилиндра, вписанного в данный конус

Решение:

Пусть задан конус высотой Н и радиусом основания R.

Обозначим через h высоту цилиндра и через r радиус

основания цилиндра, вписанного в данный конус.

Обозначим ВМ= x. Тогда

и r=R-x.

Объём цилиндра .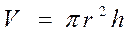

В нашем случае

Определим, при каком значении x объём цилиндра будет принимать наибольшее значение.

Найдём производную V¹ (x).

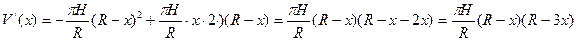
V¹(x)=0 при x=

При х< V¹(x)>0 и V¹(x) <0 при х>

Следовательно, в точке х= функция V(х) имеет максимум. Так как х может менятся от нуля до R, причём V(0)=0, то число

V()= 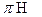R² является наибольшим значением объёма вписанных цилиндров.

Задача №7.

Найти высоту конической воронки наибольшего объёма, если её образующая равна L.

Решение.

Объём конуса,

площадь основания которого равна S,

а высота- Н, вычисляется по формуле ,

где ²,

R - радиус окружности, лежащей в основании конуса.

По теореме Пифагора R и Н связаны равенством R²+H²=L².

Воспользовавшись этим равенством, выразим V как функцию только одной переменной Н

Решая уравнения находим две критические точки функции V(H): H₁+ H_2=-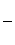

Из которых точка H принадлежит промежутку (0,L). При переходе через точку Н₁ функция V^/(H) = ( L 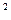-3H²) меняет знак с плюса на минус, и, следовательно, на промежутке (0, ) функция V(H) возрастает, а на промежутке (; L)убывает.

Таким образом Н= -высота конуса максимального объема при заданной длине образующей L.

Задача №8. В трапецию ABCD, боковая сторона АВ, которой

Дата добавления: 2015-01-03