
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Длина 8 см) перпендикулярна основанию, вписать прямоугольник наибольшей площади так, чтобы одна из его сторон лежала на большем основании трапеции
|
|
|
|
Длина 8 см) перпендикулярна основанию, вписать прямоугольник наибольшей площади так, чтобы одна из его сторон лежала на большем основании трапеции. Основания трапеции равны 6 и 10 см cоответственно. Вычислить площадь этого прямоугольника.
 Рассмотрим отдельно два случая.
Рассмотрим отдельно два случая.
Первый -вершина прямоугольника P лежит на боковой стороне трапеции CD.
Второй - вершина P лежит на основании трапеции ВС.
В первом случае обозначим стороны прямоугольника
|AQ|=x и |AK|=y.
Составим уравнение, связывающие неизвестные x и y.
Для этого проведем вспомогательный отрезок BL, параллельный стороне CD и рассмотрим два треугольника ABL и QPD.
Катеты этих треугольников равны соответственно
|AB|=8, |AL|=4, |QD|=10-x, |PQ|=y.
Искомое уравнение получается тогда из условия подобия треугольников ABL и QPD:
 или y=20-2x.
или y=20-2x.
Площадь прямоугольника AKPQ равна S(x)=x(20-2x).
Интервал изменения x в первом случае находится из условия, что точка Q - проекция точки P, лежащий на стороне СD, cледовательно, х  6.
6.
Таким образом, задача свелась к отысканию наименьшего значения функции S(x) на промежутке [6;10]. Единственная критическая точка функции S(x): x=5 не принадлежит найденному промежутку.
Следовательно, производная функции S(x) не меняет на этом промежутке знак.
Вычисляя производную S(x) в произвольной точке промежутка [6;10], убеждаемся, что она отрицательна.
Таким образом, наибольшее значение S(x) достигается в левом конце промежутка, т.е. max S(x)=S(6)=48см2
x 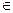 [6;10]
[6;10]
Площадь прямоугольников, относящихся по второму случаю, не превосходит 48см2, т.к. при одинаковой боковой стороне равной 8см, длины их оснований не могут быть больше 6см.
Ответ: 48см2
Задача № 9.
Из квадратного листа жести со стороной а требуется вырезать развертку правильной четырехугольной пирамиды так, чтобы вершины квадрата склеивались в вершину пирамиды. Как это сделать, чтобы получить пирамиду наибольшего объема?
Решение. Пусть АВСD - данный квадрат, О - его центры и KLMN – основание искомой пирамиды. Обозначив через К расстояние от точки К до стороны АВ, выразим объем пирамиды как функцию x.
Получим: 
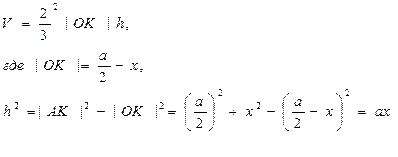

Следовательно, 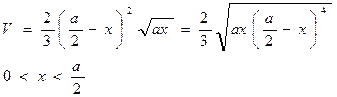
Функция принимает наибольшее значение одновременно с функцией 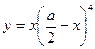 .
.
Вычислим производную:
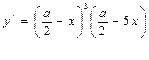


 0<x<
0<x< 
В этой задаче промежуток содержит лишь одну критическую точку. Поэтому достаточно сравнить значение функции в этой точке со значениями на концах промежутка 
Имеем, V(0)=V(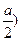 =0
=0
V(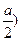 >0
>0
следовательно, при х= 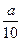 функция V имеет наибольшее значение.
функция V имеет наибольшее значение.
Таким образом, объём будет наибольшим тогда, когда диагональ её основания равна 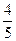 сторона квадрата.
сторона квадрата.
Задача № 10. В круг радиуса а вписан равнобедренный треугольник. При каком соотношении сторон треугольник будет иметь наибольшую площадь.
 Решение:
Решение:
 Пусть АВС=
Пусть АВС=  , тогда по теореме синусов имеем АВ=2
, тогда по теореме синусов имеем АВ=2  sin
sin  .Далее из АDC СD = АD ctg
.Далее из АDC СD = АD ctg  =
=  sin
sin 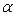 ctg
ctg  = a sin a
= a sin a  = a (1 + cos a).
= a (1 + cos a).
Рассмотрим площадь треугольника как функцию переменной а (0  ):
):
S (a) = 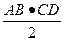 =
= 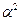 sin a (1+ cos a) =
sin a (1+ cos a) = 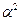 (sin a + 0,5 sin 2a).
(sin a + 0,5 sin 2a).
S` = 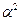 (cos a + cos 2a) =
(cos a + cos 2a) = 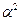 (2cos2 a + cos a – 1) =
(2cos2 a + cos a – 1) =
= a2 (cos a + 1) (2cos a – 1).
Т.к cos + 1> 0 ( (0: п)), то S` (a) = 0 при cos a = 0,5, откуда
(0: п)), то S` (a) = 0 при cos a = 0,5, откуда  .
.
Если 0 < a <  , то S` (a) > 0, т.е S (a) возрастает на
, то S` (a) > 0, т.е S (a) возрастает на
(0;  ]. Если
]. Если  < a <
< a < 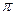 , то S` (a) < 0, т.е. S(a) убывает на [
, то S` (a) < 0, т.е. S(a) убывает на [  ;
; 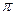 ) /
) /
Итак, max S(a) = S ( )
)
(0; 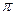 )
)
Если d =  , то треугольник равносторонний.
, то треугольник равносторонний.
Задача № 11.
Вписать в круг радиуса R прямоугольник наибольшей площади.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 629; Нарушение авторских прав?; Мы поможем в написании вашей работы!