Полезное соотношение:

Свойства дисперсии

За меру разброса случайной величины принято брать величину

- среднеквадратичное отклонение (СКО);
СКО =.
Используют также нормированное СКО ; .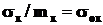

1 )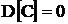 Дисперсия постоянной величины равна 0
2) Постоянный множитель выносится за знак дисперсии с возведением в квадрат.
3) 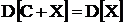Дисперсия не изменяется, если к случайной величине прибавить или отнять случайное число.
4) Если 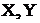- независимые случайные величины, то дисперсия суммы равна сумме дисперсий. Дисперсия разности так же равна сумме дисперсий.
;
;
.
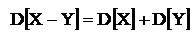5) при 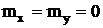. Дисперсия произведения независимых случайных величин с нулевым математическим ожиданием равна произведению дисперсий.

Дисперсия случайной величины равна математическому ожиданию квадрата этой величины за вычетом квадрата математического ожидания.

Доказательство:
.

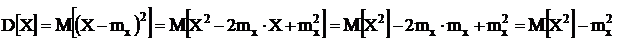Приложение к лекции
- Проведем доказательство свойства 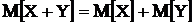на примере дискретных случайных величин. В этом случае конкретные значения, которые может принимать случайная величина Z=X+Y определяются выражением zij =(xi + yj), i = 1, 2, …, n; j = 1, 2, …, m


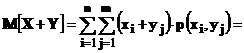
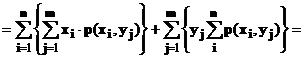
Положим, что появление значения yj это событие А и применим к этому событию формулуполной вероятности:
. *)
Событие А может появиться с одним из событий гипотез и отметим, что согласно теоремеумножения, которая была использована при выводе формулы *)
P(Hi)*P(A/Hi) = P(A*Hi)
События-гипотезы состоят в появлении значений х1, х2,...,хn. Тогда
.
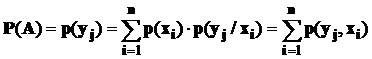Следовательно, сумма вфигурных скобках второго слагаемого должна равняться вероятности появления yj - . Тогда можно написать:

Доказательства других свойств матожидания

+
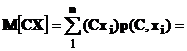
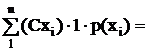
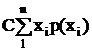
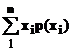
Доказательства свойства дисперсии
D[X+Y] =M[(X+Y-mx+y)2]=M[(X-mx+Y-my)2]= 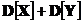+ 2M[X-mx]*M[Y-my]

18. Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Дата добавления: 2015-01-03