Пуассоновское распределение (дискретное)

Биномиальное распределение (дискретное)

III. Распределения случайных величин

Формулы по теории вероятности

В данном разделе: формулы по теории вероятностей онлайн. Полный список разделов:

· Часть 1. Случайные события

· Часть 2. Случайные величины

· Часть 3. Распределения случайных величин

· Часть 4. Другие формулы

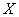- количество «успехов» в последовательности из 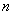независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна . .

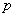Закон распределения 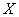имеет вид:

			…..	k	…..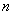

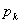
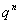
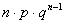
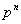
Здесь вероятности находятся по формуле Бернулли: .

Характеристики: , ,

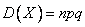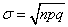
Примеры многоугольников распределения для 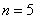и различных вероятностей:

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии 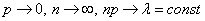закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность 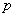события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

			…..	k	…..
			…..		…..

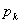
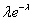
Вероятности вычисляются по формуле Пуассона: .

Числовые характеристики: , ,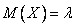

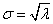
Разные многоугольники распределения при .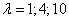

Дата добавления: 2015-01-03