Числа со знаком

Выполнение операции сложения в различных системах счисления

В десятичной системе:

1 1 - Перенос

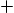4 7 9 9 + 4 = 3 + 10 (Перенос 1 в старший разряд)

3 8 4 1 + 7 + 8 = 6 + 10 (Перенос 1)

8 6 3 1 + 4 + 3 = 8

В двоичной системе:

Переполнение!

1 1 1 1 1 1 1 - Перенос

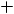1 0 1 1 0 1 0 1 = 181₁₀ 1 + 1 = 0 + 2 (Перенос 1 в старший разряд)

0 1 1 1 0 0 1 1 = 115₁₀ 1 + 0 + 1 = 0 + 2 (Перенос 1)

0 0 1 0 1 0 0 0 = 40₁₀ и так далее…

Задумайтесь над тем, почему получилось 181 + 115 = 296 – 256(?) = 40

Существует два способа представления чисел со знаком: путем выделения знакового разряда и в дополнительном коде.

При работе с восьмиразрядными целыми числами выделим старший (седьмой) разряд для хранения знака числа. Тогда, если 0000 0001 = 1, то 1000 0001 = -1. Такой подход не применяется по двум причинам:

1. Два представления 0. Если 0000 0000 = +0, тогда 1000 0000 = -0.

2. Усложнение логики процессора, так при сложении 1 и –1 должен быть получен ноль:

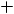0 0 0 0 0 0 0 1 = 1

1 0 0 0 0 0 0 1 = -1

1 0 0 0 0 0 1 0 = -2

- при обычной логике построения сумматора получается (-2).

Чтобы исключить эти недостатки, было разработано представление чисел в дополнительном коде.

Представление чисел в дополнительном коде основано на следующих правилах:

1. Первое правило: Для изменения знака числа необходимо проинвертировать значения разрядов числа и прибавить 1.

Например: 0000 0101 = 5

Изменим знак:

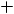Инвертируем: 1111 1010

Прибавляем 1: 1

1111 1011 = -5

2. Второе правило: Если при представлении чисел в дополнительном коде старший разряд установлен, значит, число отрицательное. Чтобы узнать его положительное значение, необходимо изменить знак числа.

Свойства чисел в дополнительном коде:

1. Единственное представление 0:

Например: 0000 0000 = 0

Изменим знак:

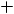Инвертируем: 1111 1111

Прибавляем 1: 1

0000 0000 = 0 - Выполняется! (Перенос игнорируем)

2. Обратимость:

Например: 1111 1011 = -5

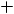Инвертируем: 0000 0100

Прибавляем 1: 1

0000 0101 = 5 - Выполняется!

3. Правильный результат операции сложения:

Необходимо, чтобы при сложении 5 и (-5) получался 0. Проверка:

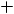0000 0101 = 5

1111 1011 = -5

0000 0000 = 0

Выполняется, однако, необходимо игнорировать возникающий перенос в несуществующий 8-й разряд и не считать такую ситуацию переполнением!

Еще примеры:

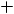
1111 1011 = -5 1111 1011 = -5 1111 1011 = -5

0000 0100 = 4 0000 0011 = 3 0000 0110 = 6

1111 1111 = -1 1111 1110 = -2 0000 0001 = 1

Если признаком того, что число отрицательное, является установленный старший разряд, тогда 0111 1111 = 127₁₀ = (2^(8-1)-1) является наибольшим положительным значением числа со знаком, а 1000 0000 = -128 = 2^(8-1) – наименьшим значением при 8-разрядном представлении чисел в дополнительном коде.

Дата добавления: 2014-12-23