Исследование свойств отношения

Построение графика.

Бинарное отношение.

Выбор варианта задания.

Анализ заданного бинарного отношения

Вариант требующего минимизации выражения бинарного отношения образуется заданием и подстановкой для шаблонной формулы: набора операций над действительными числами; набора нетривиальных операндов; бинарного отношения.

«№операций» =9mod4+1=2

№операц	a	b	g	d
Вариант2	abs	-	Æ	*

«№операндов»=9mod7+1=3

№операн	оп-д1	оп-д2	оп-д3	оп-д4
Вариант3	b-a	5*a	2*a+b	a/2

«№отношения»=24mod5+1=5

№варианта	отношение
Варіант 5	=

В шаблонную формулу

(a (Оп1 b Оп2)) Relation (g (Оп3 d Оп4))

подставляются результаты, и получается:

(abs ((b-a-5*a)) = (Æ((2*a+b)*a/2)

упрощение формулы:

| b – a – 5a | = (2a + b) ^a/2

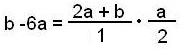
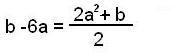
По данному отношению с помощью программ MathCad или MathLab, или же от руки, можно построить график:

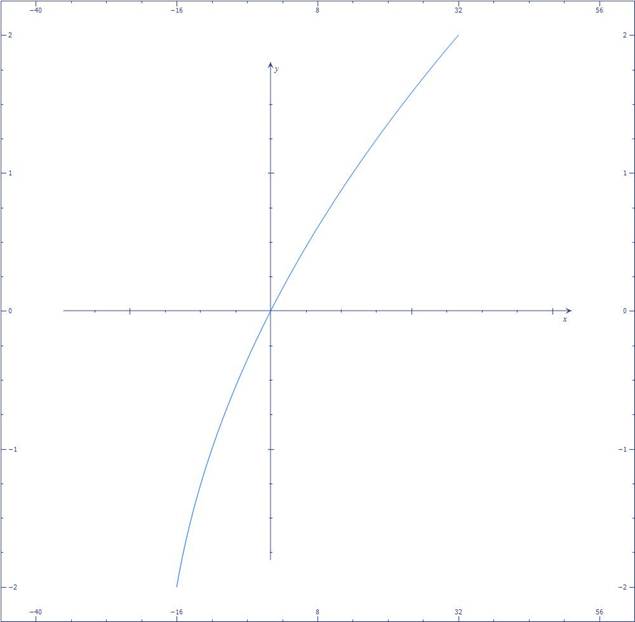
Свойства отношений доказываются путём приведения примеров на графике:

1. Функционален, так как не содержит пары с одинаковыми первыми коэфициентами
2. Инъективен, так как не содержит пары с одинаковыми вторыми компонентами «b» и разными первыми компонентами «a».
3. Не всюду определен, так как область определения не совпадает с областью отправления
4. Сюрьективен так как его область значений равна области прибытия.
5. Биективен, так как функционален, инъективен и сюрьективен.
6. Не рефлексивен так как график не содержит прямую в = а.
7. Актирефлексивен так как график содержит точки, лежащие на прямой и = а.
8. Не иррефлексивен, так как найдутся точки, принадлежащие графику и лежащие на прямой в = а.
9. Не симметричен, так как найдутся точки, не принадлежащие графику и симметричные относительно прямой в = а.
10. Не анттисимметричен, так как найдутся точки, принадлежащие графику и не симметричные относительно прямой в = а.
11. Не ассиметричен, так как найдутся точки, принадлежащие графику и симметричные относительно прямой в = а, и одновременно найдутся точки, не принадлежащие графику и симметричные относительно прямой в = а.
12. Не транзитивен.

Функциональность	+
Инъективность	+
Всюду определенность	–
Сюръективность	+
Биективность	+
Рефлексивность	–
Не рефлексивность	–
Антирефлексивность	+
Симметричность	–
Асимметричность	–
Антисимметричность	–
Транзитивность	–

Свойства отношения внесены в таблицу:

Задание № 3

Дата добавления: 2014-12-23