Анализ заданной в определенном функциональном базисе логической схемы

Вариант исходной логической схемы образуется заданием функционального базиса логических функций, размещением логических элементов в сетке мест графического изображения логической схемы, списком связей входов и выходов логических элементов.

Номер варианта заданного функционального базиса логических функций {№Ф-ции1,№Ф-ции2,№Ф-ции3} из таблицы 6, обозначаемый как «№Базиса», получается следующим образом:

«№Базиса»=(«№Зачетки»%8)+1

где % - операция получения целочисленного остатка от деления.

«№Базиса»=(9%8)+1=2, т.е. из таблицы 6 следует, что

{№Ф-ции1,№Ф-ции2,№Ф-ции3}={2,9,14}

Графическое изображение логической схемы содержит пятнадцать мест для размещения (три ряда по пять элементов) логических элементов, реализующих логические функции базиса. Элементы пронумерованы с 5 по 19 включительно, номера с 1 по 4 принадлежат входам логической схемы, а номер 20 приписан выходу всей схемы.

Номер варианта размещения логических элементов в сетке мест графического изображения логической схемы из таблицы 7, обозначаемый как «№Размещения» получается следующим образом:

«№Размещения»=(«№Зачетки»%3)+1

где % - операция получения целочисленного остатка от деления.

«№Размещения»=(9%3)+1=1, т.е из таблицы 7 получаем следующее расположение для базиса {№Ф-ции1,№Ф-ции2,№Ф-ции3}={4,6,8 }:

№элем №вар

ф-я1

x

x

x

x

x

ф-я2

x

x

x

x

x

ф-я3

x

x

x

x

x

Номер варианта списка связей входов и выходов логических элементов логической схемы обозначаемый как «№Связей» получается следующим образом:

«№Связей»=(«№Зачетки»%13)+1

где % - операция получения целочисленного остатка от деления.

«№Связей»=(9%13)+1=10

В списке связей для каждого логического элемента указаны номера логических элементов, выходы которых соединены с его входами.

Для данного варианта список связей выглядит следующим образом:

5(1,2); 6(1,2); 7(3,4,6); 8(5,6,7); 9(4,6); 10(4,7); 11(1,8,10); 12(1,9); 13(9,10); 14(9,11); 15(10,12,14); 16(10,13); 17(11,14); 18(15,17); 19(16,18); 20(18).

Полученная схема приведена ниже:

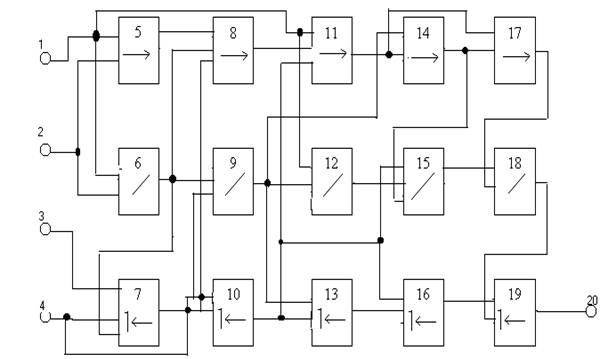
Анализ схемы.

Анализ схемы выполняется путем поэтапной подстановки выражений для реализации y

y5=x1~ x2=ùx1ùx2+x1x2

y6=x1/x2=ùx1+ùx2

y7=x3ù→x4ù→y6=(x3ùx4) ù→y6=x3x4x1x2=x1x2x3x4

y8=y5~y6~y7=((x1+x2)(ùx1+ùx2)x1x2+(ùx1ùx2+x1x2)(ùx1+ùx2)) ~y7=

=(ùx1ùx2) ~y7=(x1+x2)(ùx1+ùx2+ùx3+ùx4)+(ùx1ùx2)x1x2x3x4=x1ùx2+x1ùx3+

+x1ùx4+ùx1x2+x2ùx3+x2ùx4

y9=x4/y6 =ùx4+x1x2

y10=x4ù→y7=x4(ùx1+ùx2+ùx3+ùx4)= ùx1x4+ùx2x4+ùx3x4

y11=x1~y8~y10=(ùx1(ùx1+x2)(ùx1+x3)(ùx1+x4)(x1+ùx2)(ùx2+x3)(ùx2+x4)+

+x1(x1ùx2+x1ùx3+x1ùx4+ùx1x2+x2ùx3+x2ùx4)) ~y10=((ùx1+ùx1x2) (ùx1+x3) (ùx1+x4)(x1+ùx2)(ùx2+x3)(ùx2+x4)+(x1ùx2+x1ùx3+x1ùx4+x1x2ùx3+x1x2ùx4)) ~y10=(ùx1ùx2(ùx1+x3)(ùx2+x3)(ùx2+x4)(ùx1+x4)+ (x1ùx2+x1ùx3+x1ùx4+ +x1x2ùx3+x1x2ùx4)) ~y10=((ùx1ùx2+ùx1ùx2x3) (ùx2+x3)(ùx2+x4)(ùx1+x4)+

+(x1ùx2+x1ùx3+x1ùx4+ +x1x2ùx3+x1x2ùx4)) ~y10=((ùx1ùx2+ùx1ùx2x3)

(ùx2+x4)(ùx1+x4)+ (x1ùx2+x1ùx3+x1ùx4+ x1x2ùx3+x1x2ùx4)) ~y10=

=((ùx1ùx2+ùx1ùx2x4+ùx1ùx2x3+ùx1ùx2x3x4)(ùx1+x4)+(x1ùx2+x1ùx3+

+ x1ùx4+ x1x2ùx3+x1x2ùx4)) ~y10=(ùx1ùx2+ùx1ùx2x4+ùx1ùx2x3x4+

+ x1ùx2+x1ùx3+ x1ùx4+ x1x2ùx3+x1x2ùx4)~y10=(ùx1ùx2+x1ùx2+x1ùx3+

+x1ùx4+x1x2ùx3+x1x2ùx4) ~y10=(ùx2+x1ùx3+x1ùx4+x1x2ùx3+x1x2ùx4) ~y10=

=(ùx2+x1ùx3+x1ùx4)~y10=x2(ùx1+x3)(ùx1+x4)(x1+ùx4)(x2+ùx4)(x3+ùx4)+

+(ùx2+x1ùx3+x1ùx4)(ùx1x4+ùx2x4+ùx3x4)=x2(ùx1+x3)(ùx1ùx4+x1x4)

(x2+ùx4)(x3+ùx4) +(ùx2+x1ùx3+x1ùx4)(ùx1x4+ùx2x4+ùx3x4)=

=x2(ùx1+x3)(ùx1x2ùx4+x1x2x4+ùx1ùx4)(x3+ùx4) +(ùx2+x1ùx3+x1ùx4)

(ùx1x4+ùx2x4+ùx3x4)=x2(ùx1+x3)(ùx1x2x3ùx4+x1x2x3x4+ùx1x2x4+

+ùx1x2ùx4) +(ùx2+x1ùx3+x1ùx4)(ùx1x4+ùx2x4+ùx3x4)=(ùx1+x3)(ùx1x2x4+

+x1x2x3x4+ùx1x2x3x4) +(ùx2+x1ùx3+x1ùx4)(ùx1x4+ùx2x4+ùx3x4)=

=(ùx1+x3) (ùx1x2x4+x1x2x3x4) +(ùx2+x1ùx3+x1ùx4)(ùx1x4+ùx2x4+ùx3x4)=

=ùx1x2x4+ùx1x2x3x4+x1x2x3x4+ùx1ùx2x4+ùx2x4+ùx2ùx3x4+x1ùx2ùx3x4+

+x1ùx3x4=ùx1x2x3+x1x2x3x4+ùx2x4+x1ùx3x4

y12=x1/y9 =ùx1+x4(ùx1+ùx2)= ùx1+ùx1x4+ùx2x4=x1+ùx2x4

y13= y9ù→y10=(ùx4+x1x2)(x1+ùx4)(x2+ùx4)(x3+ùx4)=(x1ùx4+ùx4+x1x2+

+x1x2ùx4)(x2+ùx4)(x3+ùx4)=(ùx4+x1x2)(x2+ùx4)(x3+ùx4)=(x2ùx4+ùx4+

+x1x2+x1x2ùx4)(x3+ùx4)=(ùx4+x1x2)(x3+ùx4)=x3ùx4+ùx4+x1x2x3+

+x1x2ùx4=ùx4+x1x2x3

y14=y9~y11 =x4(ùx1+ùx2)(x1+ùx2+ùx4)(ùx1+ùx2+ùx3+ùx4)(x2+ùx4)

(ùx1+x3+ùx4)+(ùx4+x1x2)(ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=

=x4(ùx1ùx2+ùx1ùx4+x1ùx2+ùx2)(ùx1+ùx2+ùx3+ùx4)(x2+ùx4)(ùx1+x3+ùx4)+

+(ùx4+x1x2)(ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=x4(ùx2+ùx1ùx4)(ùx1+ùx2+

+ùx3+ùx4)(ùx1x2+x2x3+x2ùx4+ùx1ùx4+ùx3ùx4+ùx4) +(ùx4+x1x2)(ùx1x2x4+

+ x1x2x3x4+ùx2x4+x1ùx3x4)= ùx2x4(ùx1+ùx2+ùx3+ùx4)(ùx1x2+x2x3+ùx4)+

+(ùx4+x1x2)(ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=(ùx1ùx2x4+ùx2x4+

+ùx2ùx3x4)(ùx1x2+x2x3+ùx4)+ (ùx4+x1x2) (ùx1x2x4+x1x2x3x4+ùx2x4+

+x1ùx3x4)= ùx2x4(ùx1x2+x2x3+ùx4) +(ùx4+x1x2)(ùx1x2x4 +x1x2x3x4+ùx2x4+

x1ùx3x4)=(ùx4+x1x2)(ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=x1x2x3x4+

+x1x2ùx3x4=x1x2x4

y15=y10/y12/y14=((x1+ùx4)(x2+ùx4)(x3+ùx4)+x1(x2+ùx4))/y14=

=((x1x2+x1ùx4+x2ùx4+ùx4)+x1x2+x1ùx4)/y14=((x1x2x3+x1x2ùx4+x3ùx4+ùx4)+

+x1x2+x1ùx4)/y14=(x1x2+ùx4)/y14=(ùx1+ùx2)x4+(ùx1+ùx2+ùx4)=

=ùx1x4+ùx2x4+ùx1+ùx2+ùx4=ùx1+ùx2+ùx4

y16=y10ù→y13=(ùx1x4+ùx2x4+ùx3x4)x4(ùx1+ùx2+ùx3)= ùx1x4+ùx1ùx2x4+

+ùx1ùx3x4+ùx2x4+ùx1ùx2x4+ùx1ùx3x4+ùx3x4+ùx1ùx3x4+ùx2ùx3x4=

=ùx1x4+ùx2x4+ùx3x4

y17=y11~y14=(x1+ùx2+x4)(ùx1+ùx2+ùx3+ùx4)(x2+ùx4)(ùx1+x3+ùx4)

(ùx1+ùx2+ùx4)+(ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)x1x2x4=

=(x1ùx2+x1ùx3+x1ùx4+ùx1ùx2+ùx2+ùx2ùx3+ùx2ùx4+ùx1x4+ùx2x4+ùx3x4)

(ùx1x2+x2x3+x2ùx4+ùx1ùx4+x3ùx4+ùx4)+x1x2x3x4+x1x2ùx3x4=

=ùx2ùx4+x1ùx3ùx4+x1x2x3ùx4+x1ùx4+ùx1x2x4+ùx1x2x3x4+ùx1x2ùx3x4+

+x1x2x3x4+x1x2ùx3x4=ùx2ùx4+x1ùx4+ùx1x2x4+ùx1x2x3x4+ùx1x2ùx3x4+

+x2x4=ùx2ùx4+x1ùx4+x2x4

y18=y15/y17=x1x2x4+(x2+x4)(ùx1+x4)(ùx2+ùx4)=x1x2x4+(ùx1x2+x2x4+

+ùx1x4+x4)(ùx2+ùx4)=x1x2x4+(ùx1x2+x4)(ùx2+ùx4)=x1x2x4+ùx1x2ùx4+

+ùx2x4=ùx1x2ùx4+x1x4+ùx2x4

y19=y16ù→y18 =(ùx1x4+ùx2x4+ùx3x4)(ùx1+ùx2+ùx4)(x1+ùx2+x4)(x2+ùx4)=

=(ùx1x4+ùx2x4+ùx3x4)(ùx1+ùx2+ùx4)(x1x2+x1ùx4+ùx2ùx4+x2x4)=

=(ùx1x4+ùx2x4+ùx3x4)(ùx1ùx2ùx4+ùx1x2x4+x1ùx2ùx4+ùx2ùx4+x1x2ùx4+

+x1ùx4+ùx2ùx4)= (ùx1x4+ùx2x4+ùx3x4)(ùx1x2x4+ùx2ùx4+x1ùx4)=

=ùx1x2x4+ùx1x2ùx3x4=ùx1x2x4

y20=y18=ùx1x2ùx4+x1x4+ùx2x4

Теперь выполним построение сводной таблицы. В левой части таблицы приводятся все возможные наборы из четырех аргументов – от нулевого до пятнадцатого, а в правой – значения функции для каждого элемента логической схемы.

x1

x2

x3

x4

y5

y6

y7

y8

y9

y10

y11

y12

y13

y14

y15

y16

y17

y18

y19

y20

Формула ùx1x2ùx4+x1x4+ùx2x4,полученная для всей таблицы, записана в виде ДНФ. Для перевода ее в СДНФ, введем единицы для недостающих элементов в каждый минитерм:

СДНФ=(x3+ùx3)(x2+ùx2) x1x4+(x3+ùx3) ùx1x2ùx4+(x3+ùx3)(x1+ùx1)ùx2x4=

=x1x2x3x4+x1x2ùx3x4+ùx1x2x3ùx4+ùx1x2ùx3ùx4+x1ùx2x3x4+x1ùx2ùx3x4+

+ùx1ùx2x3x4+ùx1ùx2ùx3x4

Выполним перевод из CДНФ в CКНФ:

CКНФ=(ùx1+ùx2+ùx3+ùx4)(ùx1+ùx2+x3+ùx4)(x1+ùx2+ùx3+x4)(x1+ùx2+x3+x4)

(ùx1+x2+ùx3+ùx4)(ùx1+x2+x3+ùx4)(x1+x2+ùx3+ùx4)(x1+x2+x3+ùx4)

Задание № 4

Минимизация методами Квайна-МакКласки и Петрика, а также с помощью карт Карно булевой функции по исходной таблице истинности, полученной в п.4

Дата добавления: 2014-12-23