Метод Квайна-Мак-Класки

Рассмотрим функцию четырех переменных Q=f(x1,x2,x3,x4) заданную таблицей 2.

Ей соответствует дизъюнктивная совершенная нормальная форма

x1x2x3x4+x1x2ùx3x4+ùx1x2x3ùx4+ùx1x2ùx3ùx4+x1ùx2x3x4+x1ùx2ùx3x4+

+ùx1ùx2x3x4+ùx1ùx2ùx3x4

Множество 0-Кубов после разбиения и упорядочивания записывается следующим образом:

K₀=

Будем попарно сравнивать S-кубы из соседних поясов, склеивая таковые, отличающиеся только по одной координате. Такая операция склеивания соответствует объединению двух S-кубов. Получим (S+1)-куб, в котором склеиваемую координату заместим символом «~». Склеиваемые кубы будем отмечать знаком «ü».

0001ü 0100ü

0110ü 1001ü 0011ü

1101ü 1011ü

1111ü

K^’₀ =

·

~001ü 00~1ü 01~0

1~01ü 10~1ü ~011ü

11~1ü 1~11ü

K₁ =

K

~0~1

1~~1

K₂ =

K₃ = Æ

Очевидно, во множестве K₂ склеивание S-кубов невозможно. Поэтому следующее множество K₃ – пустое. Полученная сокращенная форма содержит четыре простые импликанты (неотмеченные кубы, то есть те, которые не склеились в процессе сравнения).

Теперь построим таблицу Квайна. Ее строкам соответствуют простые импликанты из сокращенной формы, столбцам – конституэнты булевой функции.

01~0	a		ü	ü
~0~1	b	ü			ü	ü		ü
1~~1	c				ü		ü	ü	ü

Очевидно, каждая импликанта является существенной. В этом случае тупиковая форма единственна. Она же будет являться и минимальной формой.

МДНФ = ùx1x2ùx4+x1x4+ùx2x4

Полученная формула в точности равна полученной еще на этапе анализа логической схемы. Действительно, при анализе мы пользовались аналитической минимизацией, применяя те ли иные свойства. Универсальный метод Квайна-Мак-Класки показал, что полученная ДНФ действительно является минимальной.

Полученный вывод можно подтвердить также с помощью метода Петрика. Логическое условие покрытия всей таблицы Квайна имеет вид:

bÙaÙaÙ(bÚc)ÙbÙcÙ(bÚc)Ùc

Производя простые преобразования, получаем:

aÚbÚc

Таким образом, с помощью метода Петрика получаем следующее выражение для МДНФ:

МДНФ = ùx1x2ùx4+x1x4+ùx2x4

Видим, что оно совпадает с выражением, полученным с помощью метода Квайна-Мак-Класки.

Теперь рассмотрим минимизацию методом карты Карно:

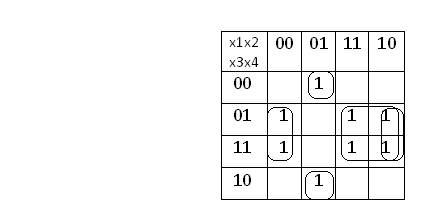
МДНФ = ùx1x2ùx4+x1x4+ùx2x4

Мы получили результат, который совпадает с двумя результатами, полученными раннее. Это говорит о правильности произведенных вычислений.

Минимизация методами Квайна-Мак-Класки и Петрика, а также с помощью карт Карно формулы частично определенной булевой функции, полученной из таблицы истинности п.4, пополненной заданными безразличными входными наборами.

Дата добавления: 2014-12-23