
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ряд динамики
|
|
|
|
Укрупненный ряд динамики
| Годы | Производство обуви | |
| Всего | Среднегодовое | |
| 1995–1997 1997–2000 | 637,6 681,6 |
В этом ряду четко прослеживается тенденция роста выпуска обуви.
Недостатком этого приема является то, что при его использовании не прослеживается процесс изменения явления внутри укрупненных интервалов.
II прием. Метод скользящей средней заключается в следующем: формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня ряда на один уровень. По укрупненным интервалам определяем среднюю из уровней, входящих в каждый интервал.
Известны следующие данные о рабочих днях и производстве продукции (табл. 5.10).
Для четкого проявления тенденции производства продукции необходимо укрупнить ряды динамики с интервалом в пять дней. Рассчитаем скользящую среднюю с интервалом в пять дней. Решение в табл. 5.10.
Таблица 5.10
| Рабочие дни | Произведено продукции, в тыс. руб. | Скользящая производства, продукции (интервал 5 дн.) | Скользящая средняя из 5 уровней |
  1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12
| 37 42 33 45 58 55 56 70 69 74 71 86 | 37+42+33+45+58=215 42+33+45+58+55=233 247 284 308 324 339 340 370 | 215: 5=43,0 233: 5=46,6 49,4 56,8 61,6 67,8 68 74 |
Получили новый РД, где четко прослеживается тенденция роста производства продукции.
Недостатки:
1. Невозможность получения всех уровней для сглаженного ряда. Число уровней в сглаженном РД меньше, чем в исходном, на (к – 1), где к – число периодов в укрупненном интервале (5 – 1) = 4, т. е. на 4.
2. Произвольность выбора интервала для определения скользящей средней.
III прием: Аналитическое выравнивание. При исчислении этого метода фактические уровни РД заменяются теоретическими, вычисленными на основе уравнения определенной кривой, отражающей общую тенденцию развития явления.
Тенденцию развития социально-экономических явлений обычно изображают кривой, параболой, гиперболой и прямой линией.
Если РД выравнивают по прямой, то уравнение прямой имеет следующий вид:
 ,
,
где у – фактические уровни;
уt – теоретическое значение уровня;
t – периоды времени – фактор времени.
«а» и «в» – параметры уравнения.
Так как «t» известно, то для нахождения «уt» необходимо определить параметры «а» и «в». Их находят способом отклонений наименьших квадратов, смысл которых заключается в следующем. Исчисленные теоретические уровни должны быть максимально близки к фактическим уровням, т.е. Sквадратов отклонений теоретических уровней от фактических должно быть 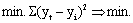
Этому требованию удовлетворяет следующая система нормальных уравнений:
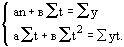
n – количество уровней РД.
Эту систему уровней можно упростить, если взять t (период времени) таким, чтобы сумма периодов равнялась нулю: Σt = 0.
Для этого необходимо периоды РД пронумеровать так, чтобы перенести в середину ряда начало отчета времени. В РД с нечетным числом периодов времени нумерация начинается с середины ряда и с нуля «0», а с четным числом периодов с «-1» и «+1». Тогда уравнения примут следующий вид:
an = Σу, отсюда получим «а»  ;
;  ,
, 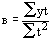 .
.
Пример: по следующим данным провести анализ основной тенденции развития явления.
Таблица 5.11
| Годы | Объем т/оборота, млн. руб. (у) | t | yt | t2 | yt | Значение теоретических уравнений |
| 1995 1996 1997 1998 1999 2000 2001 | 480 500 540 570 580 590 610 | -3 -2 -1 0 1 2 3 | -1440 -1000 -540 0 580 1180 1830 | 9 4 1 0 1 4 9 | 487,4 509,2 531,0 552,8 574,6 596,4 618,2 | 552,8 + 21,8 × (-3) = 487,4 552,8 + 21,8 × (-2) = 509,2 552,8 + 21,8 × (-1) = 531,0 552,8 + 21,8 × 0 = 552,8 |
| Σ 610 | Σуi=3869,6 |
Итого: у = 3820.
Решение задачи рассмотрим подробно:
1. Находим значение «а».
Σу = an. 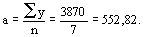
2. Для нахождения «в»:
2.1. Находим середину интервального ряда и нумеруем периоды, определяем, начиная с «0» графа 3: в = Σуt: Σуt2.
2.2. Определяем произведение уt и Σyt = 610.
2.3. Затем t2, отсюда в = 610: 28 = 21,8.
Теперь по уравнению определяем теоретические уровни (уt):
 552,8 +
552,8 +  =487,4.
=487,4.
упракт.= 3870; уt = 3869,6 расхож. мin.
Суммы теоретических и фактических уровней равны, т.е. уравнения прямой, выбранные (точно) для аналитического выравнивания, в полной степени выражают тенденцию развития изучаемого явления.
Параметры искомых уровней при аналитическом выравнивании могут быть определены по-разному. Чаще всего их определяют, решая систему нормальных уровней, полученных методом наименьших квадратов.
Аналитическое выравнивание позволяет не только определить общую тенденцию изменения явления в изучаемый период времени, но и произвести расчеты недостающих уровней рядов динамики.
Определение по имеющимся данным за определенный период времени недостающих значений признака внутри периода называется интерполяцией. Нахождение значений признака за пределами анализируемого периода называется экстраполяцией. Экстраполяция может осуществляться как в прошлое, так и в будущее.