Способы распространения результатов выборочного наблюдения на генеральную совокупность

Способ прямого пересчета в том, что при нем показатели выборочной доли w или средней х распространяются на генеральную совокупность с учетом ошибки выборки.

Выборочный метод применяется для получения характеристик генеральной совокупности по определенным показателям выборки. В зависимости от целей исследования это осуществляется прямым пересчетом показателей выборки для генеральной совокупности или методом расчета поправочных коэффициентов.

Способ поправочных коэффициентов применяется, когда целью выборочного метода является уточнение результатов сплошного учета. Данный способ используется при уточнении данных ежегодных переписей скота у населения.

Способы зависят от целей:

1. Цель – определение обобщающих показателей генеральной совокупности.
• Метод – устанавливаются предельные значения и доверительный интервал для показателей генеральной совокупности.

2. Цель – определение объема признака для генеральной совокупности по результатам выборки.
• Метод – производится прямой пересчет показателей выборки на генеральную совокупность.

3. Цель – уточнение результатов сплошного наблюдения.
• Метод – используется способ поправочных коэффициентов.

Характеристика генеральной совокупности на основе выборочных результатов – это конечная цель выборочного наблюдения.

Выборочный метод применяется для получения характеристик генеральной совокупности по определенным показателям выборки. В зависимости от целей исследования это осуществляется прямым пересчетом показателей выборки для генеральной совокупности или методом расчета поправочных коэффициентов.

Способ прямого пересчета в том, что при нем показатели выборочной доли w или средней х распространяются на генеральную совокупность с учетом ошибки выборки.

Способ поправочных коэффициентов применяется, когда целью выборочного метода является уточнение результатов сплошного учета. Данный способ используется при уточнении данных ежегодных переписей скота у населения.

61) Необходимый объем выборки

Определение необходимого объема выборки играет чрезвычайно важную роль в статистических исследованиях. Необходимый объем выборки представляет собой достаточный объем выборки, позволяющий по характеристикам отобранной части единиц судить о характеристиках всей совокупности. Необходимая численность выборки может быть определена на базе допустимой (предельной) ошибки при выборочном наблюдении или на базе способа отбора. Рассматривая величину необходимой численности выборки в общем виде (задавая величину допустимой ошибки), исследуются в дальнейшем особые условия, создающиеся в процессе вычисления при разных способах отбора.

Из формулы предельной ошибки, которая определяется как:

численность случайной выборки (n) получается равной:

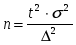(8.1)

Из этой формулы, в частности, следует, что при увеличении возможной (приемлемой) ошибки выборки значительно уменьшается необходимый объем выборки. Так, при увеличении допустимой ошибки в два раза, необходимый объем выборки уменьшается в четыре раза.

Из формулы (8.1) видно, что необходимый объем выборки пропорционален показателю 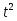и дисперсии признака .

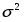Необходимая численность выборки рассчитывается по-разному для выборочного наблюдения, в котором устанавливается средний размер признака в совокупности, и для наблюдения, в котором определяется доля единиц, обладающих данным признаком. Это происходит в силу различных методов вычисления меры колеблемости для варьирующего и альтернативного признака.

Очень часто трудно определить необходимый объем выборки. Это связано с тем, что недостаточно разработаны такие вопросы, как оценка вариации изучаемых признаков, обоснование численности выборки при изучении нескольких признаков, зависимость объема выборочной совокупности от программы разработки материалов наблюдения и пр.

Трудности порождаются еще и тем, что кроме чисто статистических в определении необходимого объема выборки большое значение принадлежит факторам организационного порядка, которые обязательно должны быть учтены. К ним относится и обеспеченность ресурсами, длительность обработки и срочность представления результатов и т.д.

Одним из наиболее важных и в то же время сложных вопросов определения необходимого объема выборки является расчет показателя вариации изучаемого признака (). При организации выборочного наблюдения еще отсутствуют необходимые данные. Основой оценки колеблемости изучаемого признака служат, как правило, материалы предыдущих обследований. Следует иметь ввиду, что использование данных прошлых обследований имеет смысл только тогда, когда за прошедший с момента последнего обследования период в генеральной совокупности не произошло существенных изменений.

Иногда для определения коэффициента вариации проводится пробное обследование. По данным предварительного или пробного обследования рассчитывается среднее квадратическое отклонение и дисперсия признака для определения и обоснования необходимого объема выборки. Если мера колеблемости признака неизвестна, то ее можно найти приближенно по величине предполагаемого размаха или среднего линейного отклонения по следующим формулам:

(8.3)

(8.4)

где - среднее квадратическое отклонение;

R - размах вариации;

- среднее линейное отклонение.

Для расчетов величины выборки при различных значениях коэффициента t и различных значений вероятности рассчитаны специальные таблицы соответствия. В частности, при:

t = 1 Ф (t) = 0.683 t = 1.5 Ф (t) = 0.866

t = 2 Ф (t) = 0.954 t = 2.5 Ф (t) = 0.988

t = 3 Ф (t) = 0.997 t = 3.5 Ф(t) = 0.999

Важным условием практического использования формул (8.2) и (8.3) является близость фактического распределения к нормальному. Для несимметричных распределений применение их не имеет смысла.

При статистическом исследовании многих массовых явлений и процессов приходится сталкиваться с качественными признаками. Например, признак пола при проведении обследований населения. Тем не менее по качественным признакам также можно определить необходимый объем выборки. Способ выражения качественных признаков не позволяет рассчитать по ним средние значения, поэтому оценка колеблемости производится, как правило, исходя из долей единиц, обладающих значениями этих признаков. Такие доли называются выборочными долями или частостями.

Если расчет проводится по качественному альтернативному признаку и неизвестна его доля в генеральной совокупности, то рекомендуется принять ее равной 0.5, так как дисперсия доли при этом достигает максимума 0.25. Для неальтернативных признаков использовать формулу нельзя.

Преимущество такого приема заключается в том, что он позволяет определить численность выборочной совокупности, не располагая данными предыдущих обследований, и не проводить пробных обследований.

В ряде случаев приближенная оценка колеблемости признака может быть осуществлена с помощью превращения изучаемого признака в альтернативный. Но нужно учитывать, что такое превращение приводит к потере части информации. Например, все категории занятых на производственном предприятии могут быть разделены условно на две группы - рабочие и служащие. Однако при этом из анализа выпали другие категории работников: охрана, МОП и др., которые выделяются в отдельные самостоятельные группы. Прием превращения признака в альтернативный возможно применять только в случае, если существует уверенность о незначительной доле неучтенных единиц во всей совокупности. В Таблице 8.1 приведены некоторые формулы расчета объема выборки, наиболее часто используемые в практике.

Необходимый объем выборки для некоторых способов формирования выборочной совокупности

Таблица 8.1.

Виды выборочного наблюдения	Повторный отбор	Бесповторный отбор
Собственно-случайная выборка:
а) при определении среднего размера признака
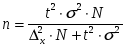
б)при определении доли признака
^ Механическая выборкаТипическая выборка	то же	то же
а) при определении среднего размера признака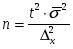
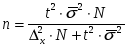
б) при определении доли признака
^ Серийная выборка
а) при определении среднего размера признака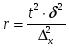
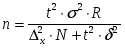
б) при определении доли признака

Пример. В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0.8 человека с вероятностью Ф(t)=0.954 и при среднем квадратическом отклонении 3.0 человека (ошибка и среднее квадратическое отклонение определены на основе пробного обследования).

Так как при Ф(t)=0.954 t=2, то в этом случае необходимая численность выборки равна:

62) Для описания причинно-следственной связи между явлениями и процессами используется деление статистических признаков, отражающих отдельные стороны взаимосвязанных явлений, нафакторные и результативные. Факторными считаются признаки, обуславливающие изменение других, связанных с ними признаков,являющихся причинами и условиями таких изменений. Результативными являются признаки, изменяющимися под воздействием факторных.

Формы проявления существующих взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную и статистическую связи.

Функциональной называют такую связь, при которой определённому значению факторного признака соответствует одно и только одно значение результативного. Такая связь возможна приусловии, что на поведение одного признака (результативного) влияеттолько второй признак (факторный) и никакие другие.Такие связи являются абстракциями, в реальной жизни онивстречаются редко, но находят широкое применение в точных науках и впервую очередь, в математике. Например: зависимость площади круга отрадиуса: S=π∙ r 2

Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы изучаемой совокупности. В массовых явлениях проявляются статистические связи, при которых строго определённому значению факторного признака ставится в соответствие множество значений результативного. Такие связиимеют место, если на результативный признак действуют несколькофакторных, а для описания связи используется один или несколькоопределяющих (учтённых) факторов.

Строгое различие между функциональной и статистической связью можно получить при их математической формулировке.

Функциональную связь можно представить уравнением: вследствие действия неконтролируемых факторов или ошибок измерения.

Примером статистической связи может служить зависимость себестоимости единицы продукции от уровняпроизводительности труда: чем выше производительность труда, тем ниже себестоимость. Но на себестоимость единицы продукции помимо производительности труда влияют и другие факторы: стоимость сырья, материалов, топлива, общепроизводственные и общехозяйственные расходы и т.д. Поэтому нельзя утверждать, что изменение производительности труда на 5% (повышение) приведет к аналогичному снижению себестоимости. Может наблюдаться и обратная картина, если на себестоимость будут влиять в бóльшей степени другие факторы, - например, резко возрастут цены на сырье и материалы.

Любую статистическую связь можно представить в виде набора локальных распределений результативного признака при фиксированных значениях факторного:

Корреляционная связь проявляется только на всей статистической совокупности, а не в каждом отдельном случае, так как только при достаточно большом числе случаев каждому случайному значению факторного признака будет соответствовать распределение средних значений случайного признака y.

По направлению корреляционные связи делятся на прямые и обратные. При прямой связи результативный признак растёт сувеличением факторного, при обратной - рост факторного признакаприводит к снижению значений результативного признака. Например, чембольше стаж работы, тем выше производительность труда – прямая связь,а чем выше производительность труда, тем ниже себестоимость единицыпродукции – обратная связь.

По форме (аналитическому выражению) связи делятся на линейные (прямолинейные) и нелинейные (криволинейные) связи. Линейные связи выражаются уравнением прямой, а нелинейные – уравнением параболы, гиперболы, степенной и т. п.

По количеству взаимодействующих факторов связи делятся на парную (однофакторную) и множественную (многофакторную) связи. При парной связи на результативный признак действует один факторный, при множественной – несколько факторных признаков. Исследование статистической связи проводится в следующемпорядке:

􀂃 качественный анализ связи - определение состава признаков, предварительный анализ формы связи;

􀂃 сбор данных на основе статистического наблюдения;

􀂃 количественная оценка тесноты связи по эмпирическим данным;

􀂃 регрессионный анализ (аналитическое описание связи):

- выбор формы связи,

- оценка параметров модели,

- оценка качества модели.

Основным методом изучения статистической взаимосвязи является статистическое моделирование связи на основе корреляционного и регрессионного анализа. Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками при парной связиили между результативным и несколькими факторными примножественной связи. Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии. Регрессией называетсязависимость среднего значения случайной величины результативногопризнака от величины факторного, а уравнением регрессии – уравнениеописывающее корреляционную зависимость между результативным признаком и одним или нескольким факторными.

63) Криволине́йная систе́ма координа́т, или криволине́йные координа́ты в математике — система координат в евклидовом (аффинном) пространстве, или в области, содержащейся в нём. Криволинейные координаты противопоставляются прямолинейным: декартовым, а также косоугольным. Применяются обычно на плоскости (n =2) и в пространстве (n =3); число координат равно размерности пространства n. Наиболее известным примером криволинейной системы координат являются полярные координаты на плоскости.

Локальные свойства криволинейных координат[править | править исходный текст]

При рассмотрении криволинейных координат в данном разделе мы будем полагать, что рассматриваем трёхмерное пространство (n =3), снабженное декартовыми координатами x, y, z. Случай других размерностей отличается лишь количеством координат.

В случае евклидова пространства метрический тензор, именуемый также квадратом дифференциала дуги, будет в этих координатах иметь вид, соответствующий единичной матрице:

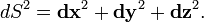
Общий случай [править | править исходный текст]

Криволинейные координаты в трёхмерном аффинном пространстве

Пусть , , 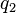— некие криволинейные координаты, которые мы будем считать заданными гладкими функциями от x, y, z. Для того, чтобы три функции , , 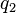служили координатами в некоторой области пространства, необходимо существование обратного отображения:

где — функции, определённые в некоторой области наборов координат.

Дата добавления: 2014-12-24