Простые и сложные гипотезы и их проверка

Статистические гипотезы

Как отмечалось выше, в математической статистике считается, что данные, получаемые в результате наблюдений, подчинены некоторому неизвестному вероятностному распределению, и задача состоит в том, чтобы извлечь из данных правдоподобную информацию об этом неизвестном распределении. В настоящей главе мы обсудим еще один подход к этой общей задаче, состоящий в проверке гипотез. Статистической гипотезой называют предположение о распределении вероятностей, которое необходимо проверить по имеющимся данным.

Параграфы этой главы:

Пусть 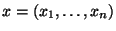-- независимая выборка, соответствующая неизвестной функции распределения . Простой гипотезой называют предположение, состоящее в том, что неизвестная функция отвечает некоторому совершенно конкретному вероятностному распределению. Пример простой гипотезы:

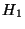: данные являются выборкой из равномерного распределения
в отрезке .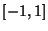

Сложной гипотезой называют предположение о том, что неизвестная функция принадлежит некоторому множеству распределений, состоящему из более чем одного элемента. В качестве иллюстрации можно привести Пример 6.3.

Проверить статистическую гипотезу 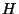-- это значит на основе имеющихся данных 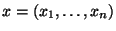принять или отвергнуть сделанное предположение. Для этого используется подход, основанный на выборе так называемого критического множества 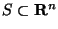. Мы поступаем следующим образом: если данные наблюдений попадают в критическое множество (то есть, 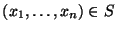), то гипотеза 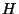отвергается; если же данные находятся вне критического множества (то есть, 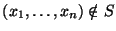), то гипотеза 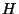принимается. Такое решающее правило будем называть критерием, основанным на критическом множестве .

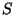Существует много методов построения критических множеств для проверки статистических гипотез, некоторые из этих методов обсуждаются в последующих параграфах. Сейчас мы кратко коснемся вопроса о возможных ошибках, которые мы допускаем, принимая или отвергая гипотезы.

В силу случайной природы наблюдаемых данных возможна ситуация 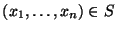в то время, когда гипотеза 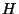справедлива. Однако, согласно решающему правилу, в этом случае мы отвергнем верную гипотезу 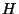и, тем самым, допустим ошибку. Очевидно, что в случае простой гипотезы 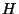вероятность такой ошибки равна . Эту вероятность называют также уровнем значимости статистического критерия. Такого рода ошибки неизбежны при анализе случайных данных, и их не следует драматизировать. На практике уровень значимости критерия задается изначально, исходя из реальных приложений и потенциальных последствий возможных ошибок.

Дата добавления: 2014-12-24